APLICAȚII (CODA & APENDICE)

CODA
Am amânat în mod persistent finalizarea acestui ultim expozeu aplicativ pentru că abordarea temelor complexe cere un efort de sinteză mult mai susținut decât m-am așteptat, dar, în mod paradoxal, și o pregătire analitică mult mai exactă prin selectarea celor mai concise variante de deconstrucție și contiguitate ale suprafețelor. Cu toate acestea, încă am rezerve și cred că este încă loc de o abordare mult mai directă, chiar și cu riscul sacrificării exactității geometrice. Aplicarea metodei medianei sugerează o apropiere mai mare de obiectivul unei abordări pur observaționale în cercetarea vizual-structurală morfologică, datorită reducerii prelucrării suprafețelor. Această abordare rămâne însă un obiectiv pentru un viitor mai îndepărtat, datorită complexității informației analitice și a nevoii unor noi criterii de reducție mai cuprinzătoare – cum ar fi cele statistice.
După cum am amintit în observațiile finale din prima parte a aplicațiilor, este nevoie de o simplificare consistentă a etapelor, chiar dacă acest lucru înseamnă o concentrare a analizei în fazele care inițial erau destinate sintezei moorfologice. Pentru aceasta am renunțat la vectorializarea limitelor și la elementarizarea conținuturilor. Inițial am crezut că tendințele de elementarizare dimensională a suprafețelor vor ajuta la indicarea obiectelor morfologice prin recesivitate dimensională și prin alternanță dimensională între fond-obiect-fond, dar vectorialitatea limitelor nu are ca și consecință directă determinarea sensului conținutului obiectului morfologic.
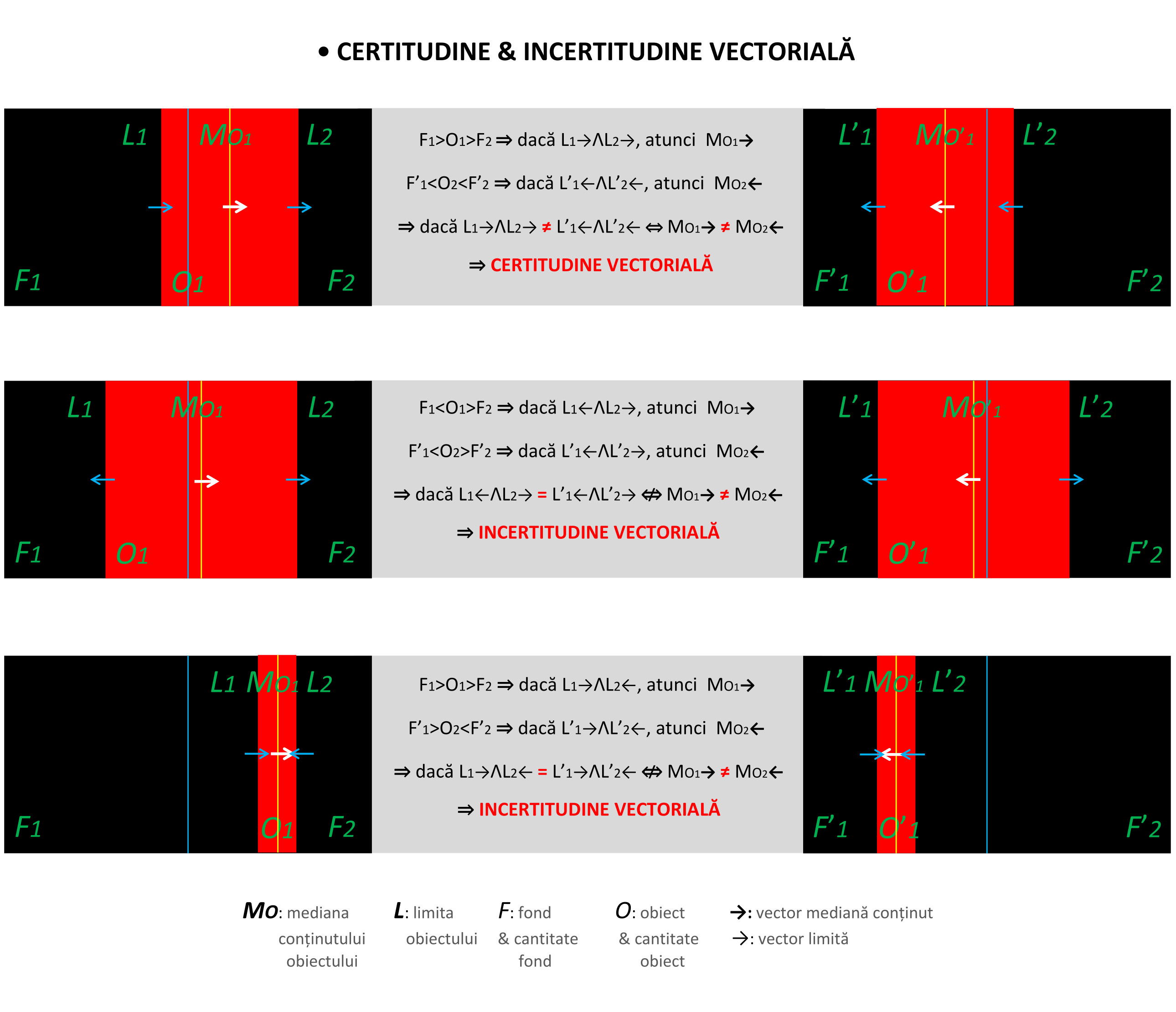
El poate fi determinat mult mai exact prin plasarea medianei obiectului, raportat la plasarea medianei supafeței de bază în care este inclus obiectul și fondul, complementar pe direcția traseului lor de coliniaritate.
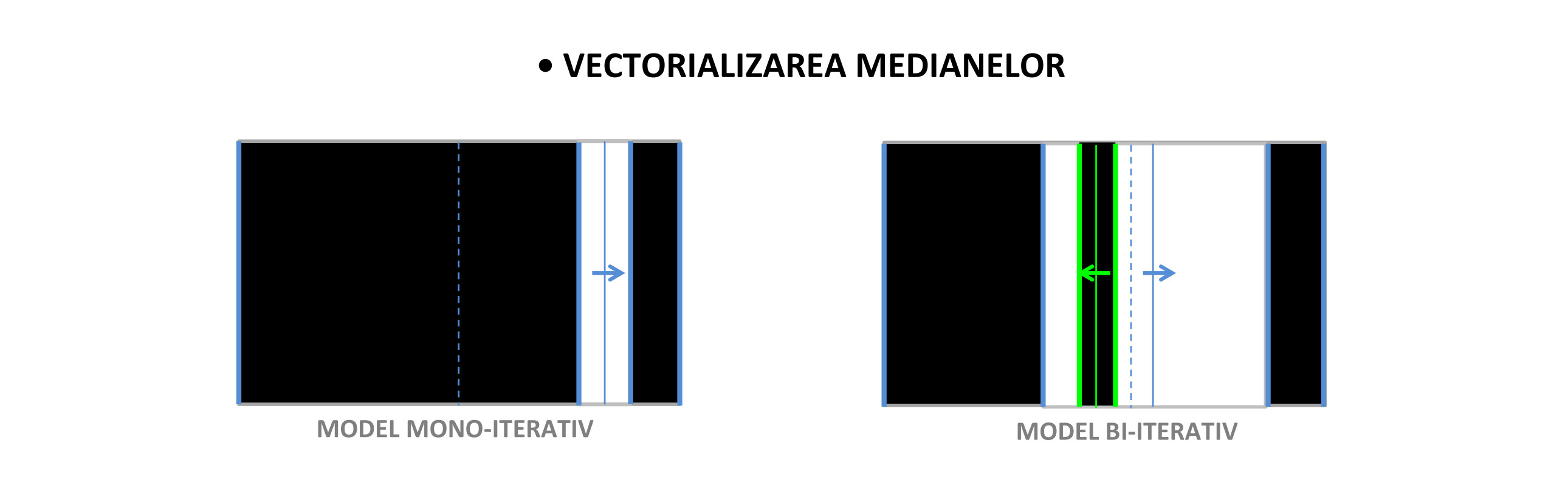
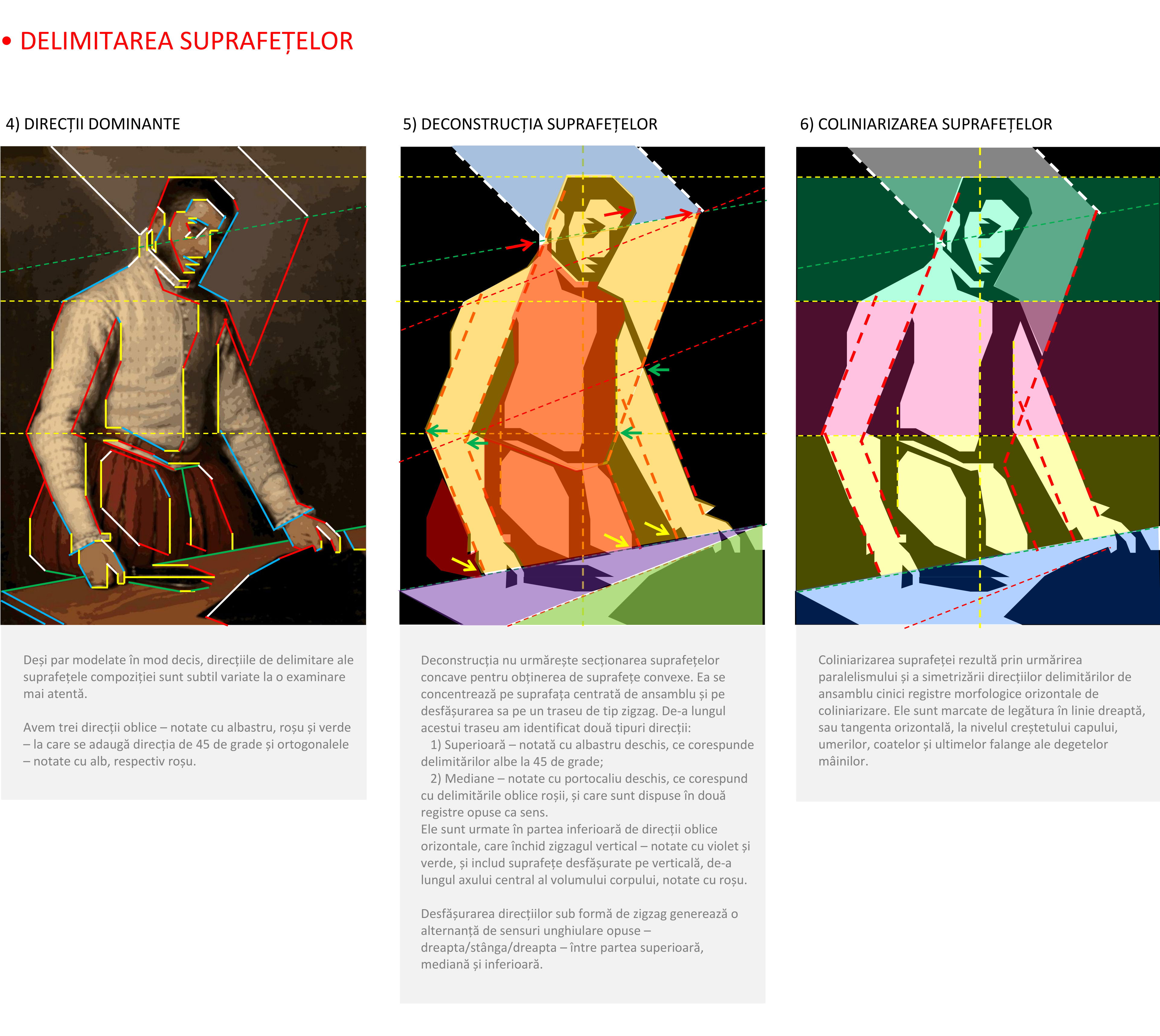
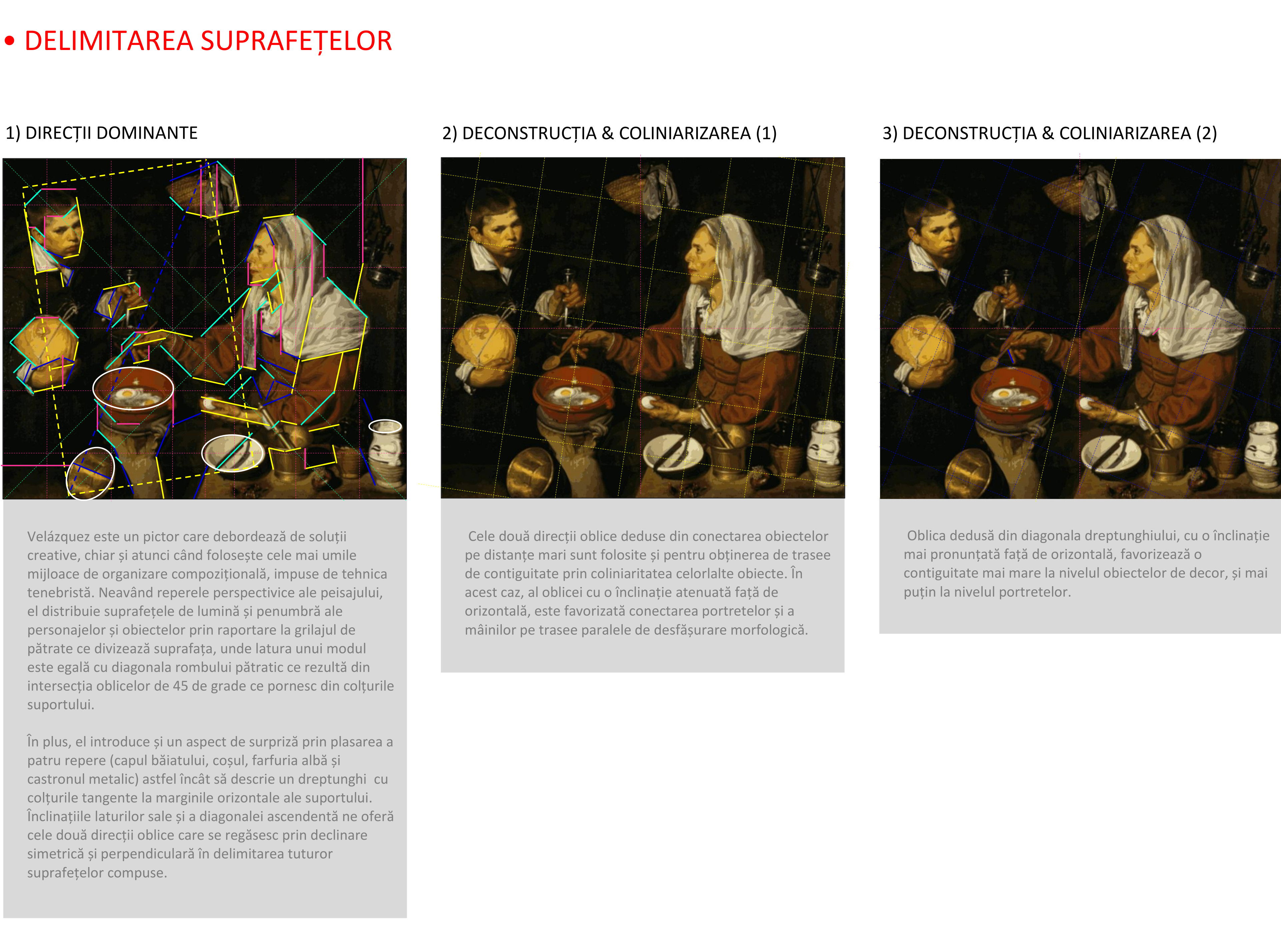
Accentul cade în delimitarea suprafețelor pe categoriile de direcții rectiliniare oblice adoptate prin simplificarea delimitărilor reale ale suprafețelor hărții cromatice. Fragmentarea complexă a suprafețelor, reclamă însă deducerea lor din relațiile geometrice de ansamblu ale rețelei de trasee proprii suportului de lucru. De asemenea, hărțile cromatice pot fi simplificate prin înlocuirea diversității tonale și a categoriilor cromatice cu relații de polaritate valorică, contrast saturativ, și contrast caloric, reliefat prin integrare izovalorică, cu dominantă închisă sau deschisă.
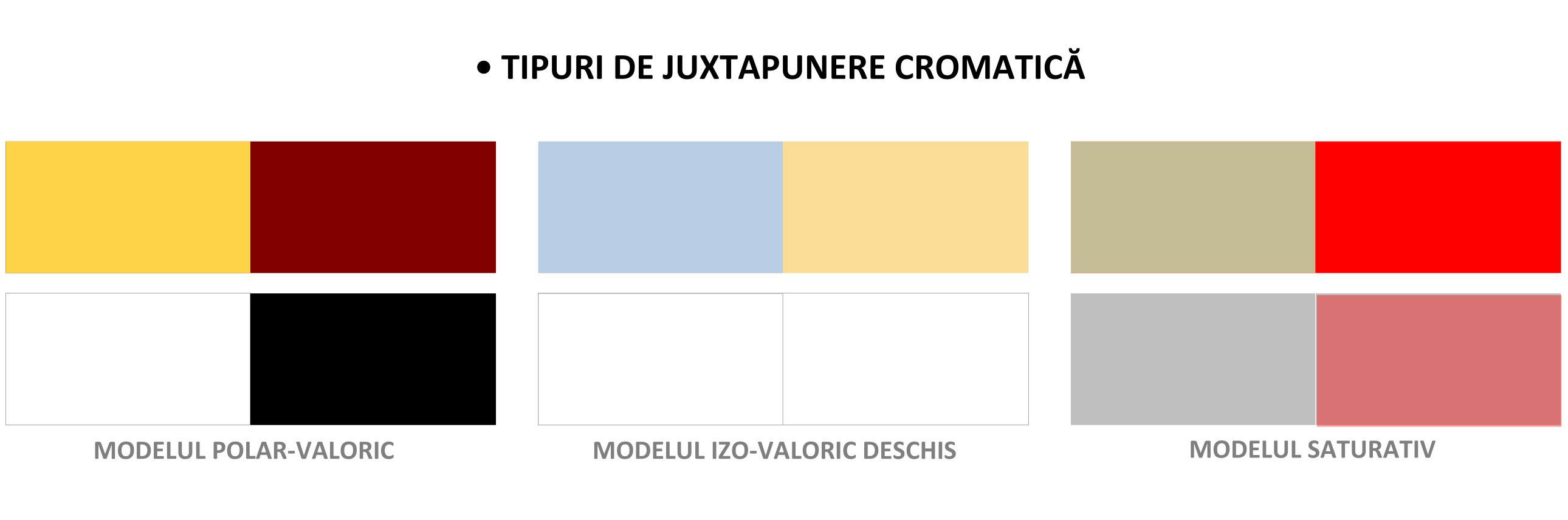
Pentru a concentra inițierea etapelor sintetice, deconstrucția suprafețelor poate fi unită cu coliniarizarea suprafețelor. La acest nivel incipient de morfologizare a construcției nu există soluții unice, ci multiple posibilități de rezolvare în orizontul eleganței și unității de contiguitate a organizării suprafețelor în trasee de coliniaritate cât mai cuprinzătoare și ușor de descifrat morfologic.
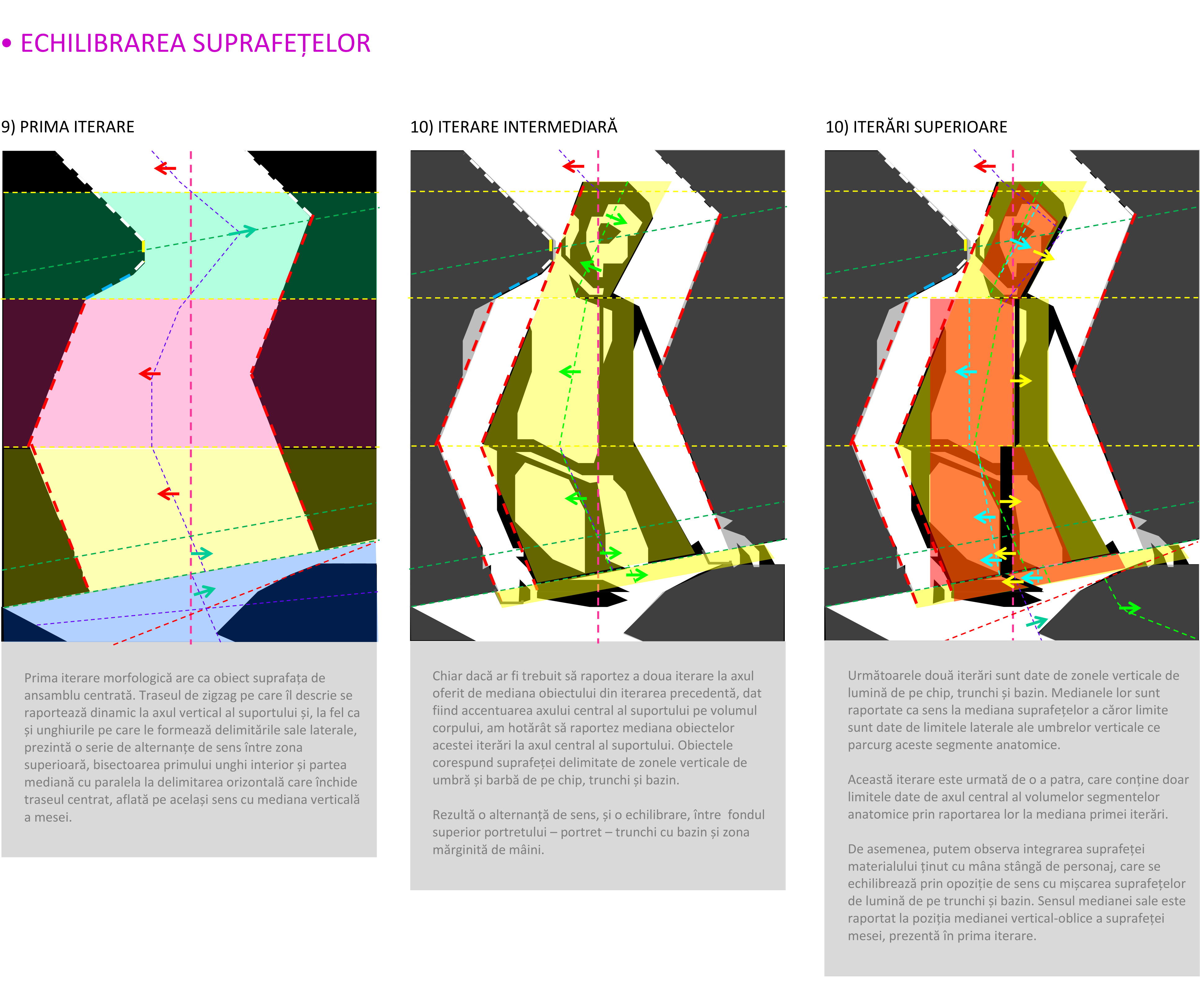
Echilibrul iterărilor morfologice este stadiul final al esențializării sintezei morfologice a construcției, concretizată prin descifrarea sensului și ierarhiei obiectelor. Din punct de vedere ierarhic, fiecare formă este plasată în straturi atentiv-selective numite iterări morfologice, astfel încât rezultă trei tipuri de conectări în te forme și obiecte:
1) co-iterative, când obiectele sunt plasate în forme dezvoltate la același nivel iterativ, dar în componente morfologice distincte ale aceleiași forme de bază;
2) trans-iterative, când obiectele sunt plasate în iterări distincte, dezvoltate în componente morfologice distincte ale formei de bază;
3) infra-iterative, când obiectele sunt plasate în forme dezvoltateîn iterări succesive și recurente, incluse în aceeași componentă morfologică a formei de bază.
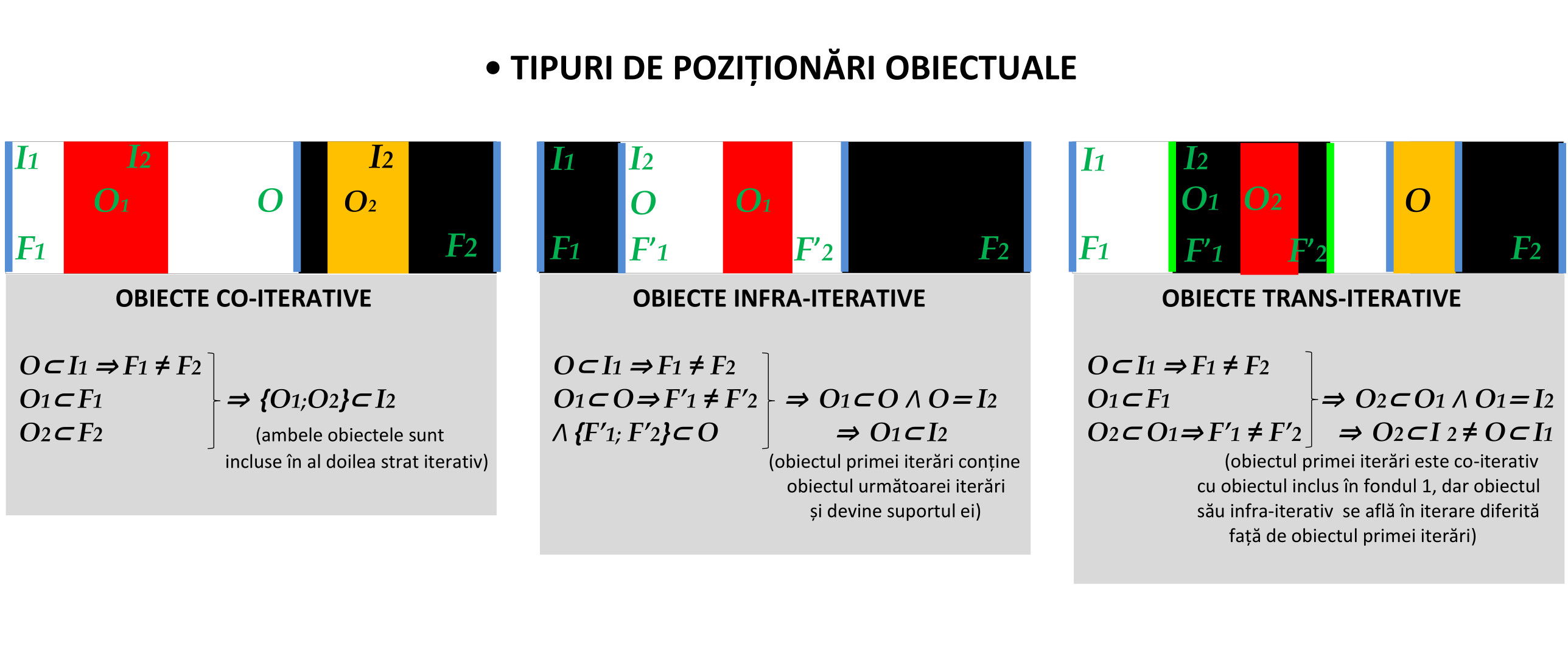
Respectând aceste simplificări în etapele de cercetare morfologică, tot șirul laborios de doisprezece etape poate fi redus doar la patru sau cel mult șase etape. Vom vedea, însă, că nu există un traseu prestabilit de descifrare morfologică în temele complexe. Fiecare lucrare și fiecare autor are procedeele sale particulare de compartimentare morfologică, mai mult sau mai puțin accesibile prin reducție. Ele depind de interesele vizuale pentru materialul constructiv al compoziției.










APENDICE
Înainte de stabilirea metodei vectoriale, aplicată limitelor și conținuturilor suprafețelor în contextul compozițional al variațiilor cantitative, am încercat să rezolv problema exprimării contextului compozitional prin alte metode cu caracter matematic și măsurabil sau enumerativ mai pronunțat și non-dinamic. Principalele indicii constructive în definirea matematică a formei la momentul respectiv erau: caracterul fractalic, datorat aprofundării iterative a componentelor morfologice, și manifestarea contextual-dimensională a modelării suprafețelor compoziției. În prima tendință se încadrează metodele de dimensionalizare fractalică și de compartimentare a suprafețelor prin nesting și packing, în timp ce a doua tendință cuprinde metoda transformării suprafețelor. Ca metodă mixtă, care îmbină recurența fractalilor și dimensionalizarea geometrică a suprafețelor, avem complexul elementar-dimensional, care a dus la nevoia descoperirii metodei vectoriale.
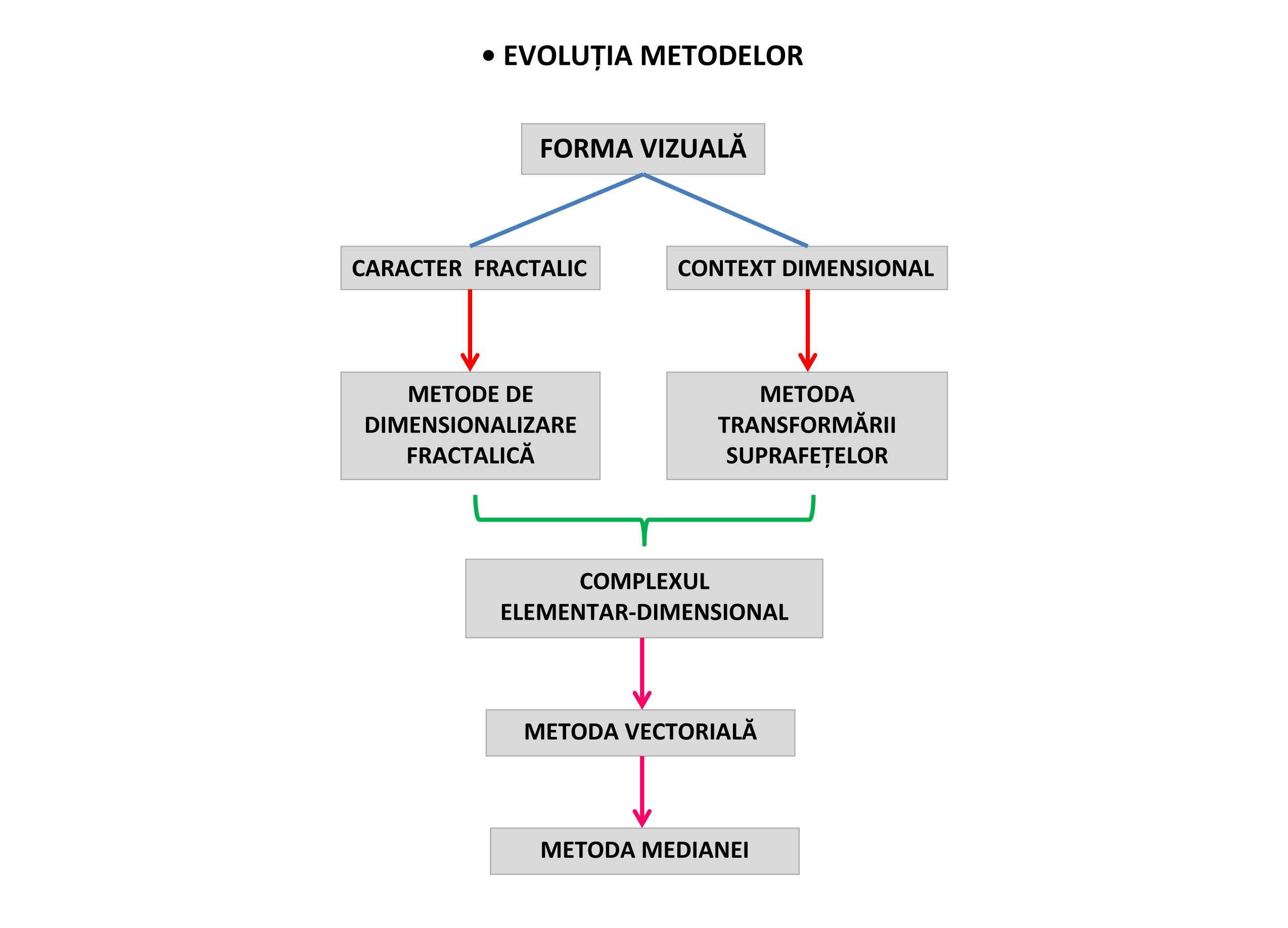
În cele din urmă, doar metoda vectorială și în special metoda medianei s-au dovedit a fi cele mai potrivite pentru exprimarea esențializată a mișcării implicite a suprafețelor în contextul compozițional, datorită caracterului lor sintetic. Aplicarea metodelor scalare și a celor transformative s-a dovedit a fi prea vagă, respectiv, prea rigidă și, în consecință, incompatibilă cu aprofundarea sintetică și esențializator-reductivă a relațiilor dintre suprafețe în contextul compozițional.
1) Dimensionalizare fractalică
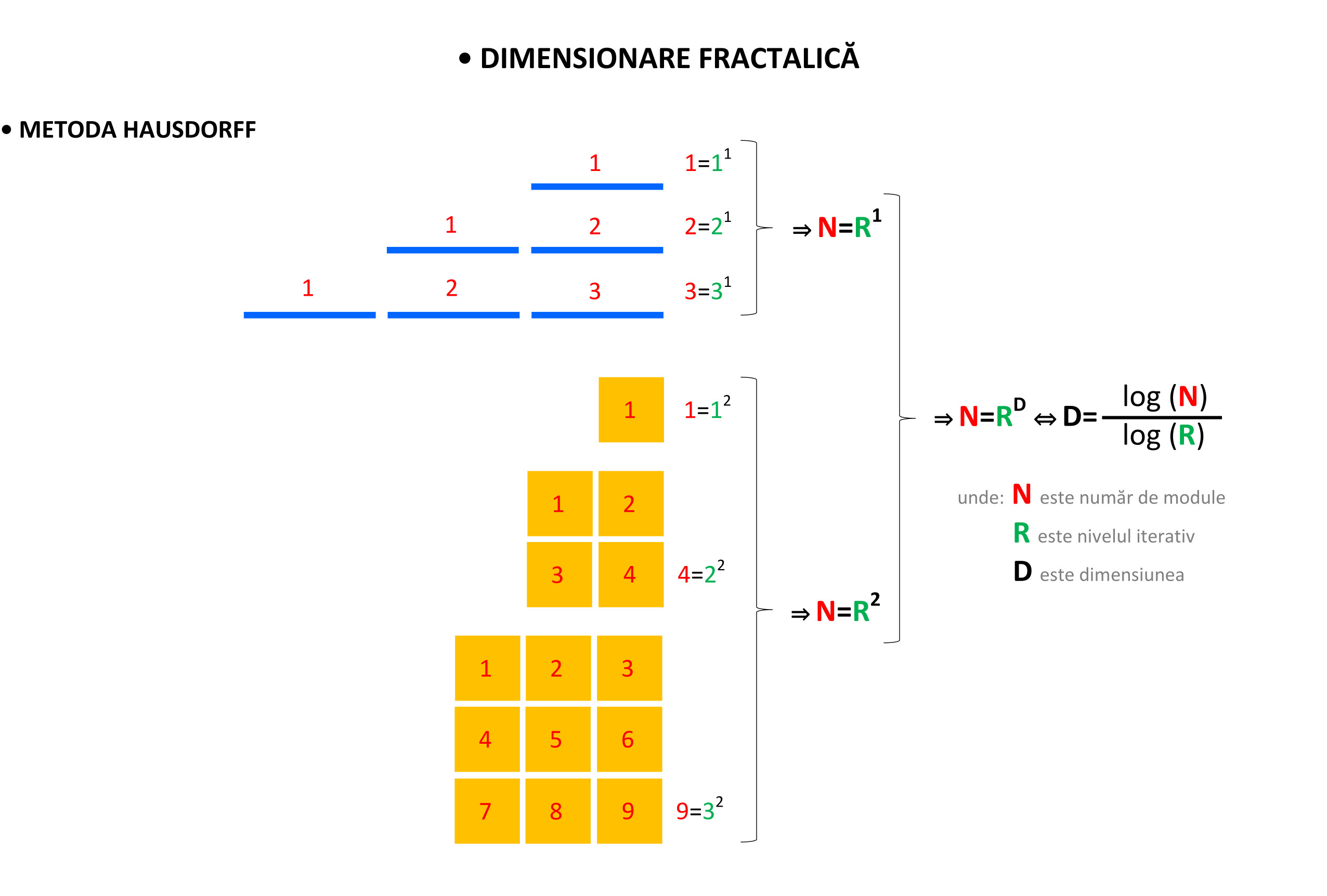
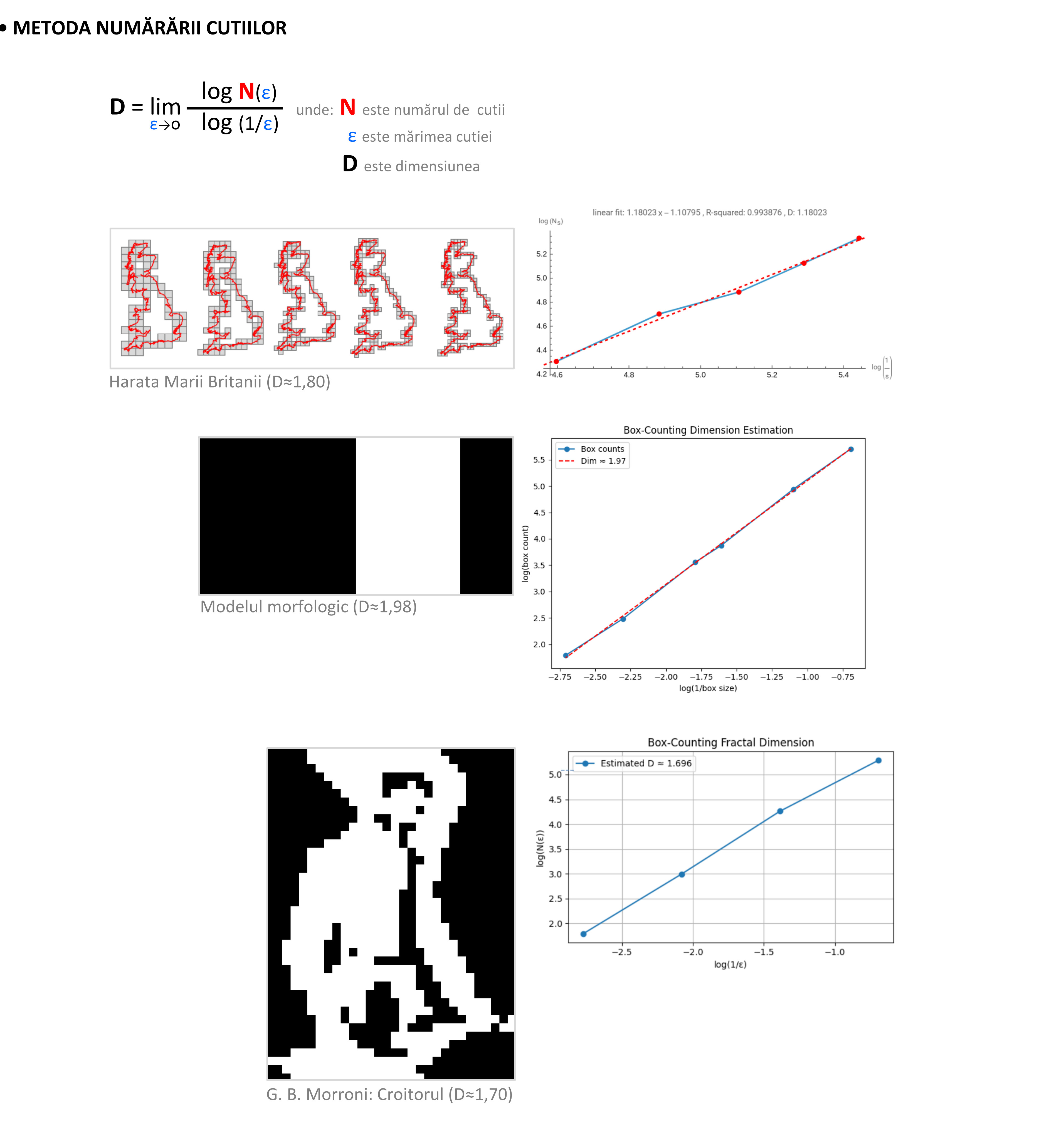
Dată fiind organizarea modulară a construcției componentelor morfologice, putem să descriem forma vizuală ca fiind un fractal scalar monodimensional, unde, în loc de segmente de dreaptă, avem ca modul dreptunghiuri. În acest caz am aplica metoda Hausdorff de calculare a dimensiunii fractalice prin scalarizare, iar dimensiunea sa ar fi egală cu 1. De asemenea, dacă prin polarizare valorică ar obținem un obiect alb și suprafețe de fond negre, unde raportul dintre suprafețele negre și suprafața albă ar fi exprimat folosind metoda enumerării cutiilor, va rezulta o dimensiune aproximativ egală cu 1,98.
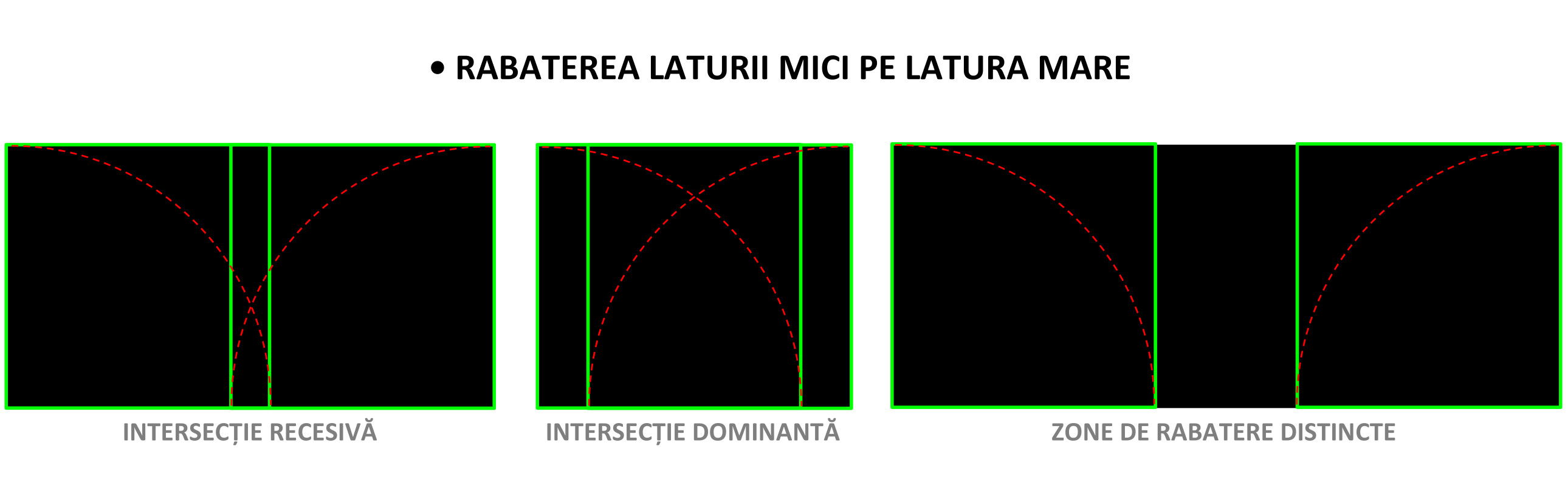
Ca aprofundare a metodei Haudorff, se pot folosi și metode de compartimentare deconstructivă a suprafețelor prin rabaterea laturii mici pe latura mare a dreptunghiului sau prin metode de nesting și packing. Nesting presupune eficientizarea spațiului conținutului de suprafață compartimentat, în timp ce packing se bazează pe valorificarea a cât mai mult spațiu posibil, ducând la un grad mai ridicat de umplere al conținutului.
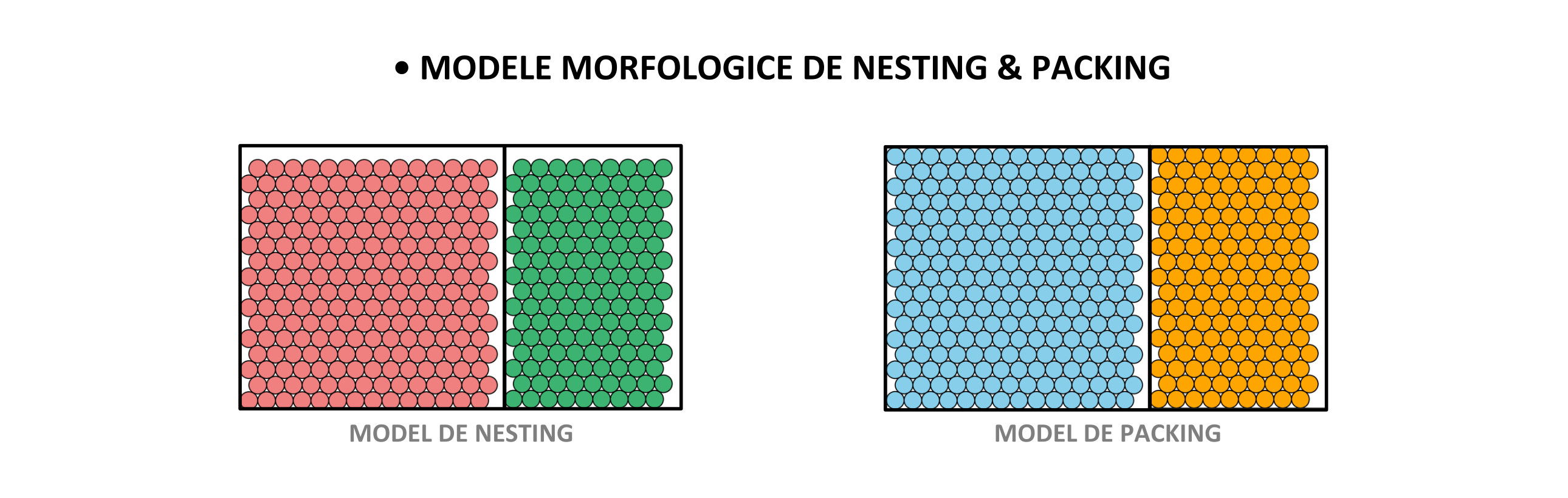
Exprimarea algebrică a gradelor de acoperire a unei suprafețe morfologice, față de altă suprafață, deși pot fi comparate dimensional, nu pot descrie poziționarea și dinamica modelării suprafețelor. De altfel, la momentul propunerii acestor metode, dinamica suprafețelor era doar intuită.
2) Transformarea suprafețelor
Ce se întâmplă dacă îngustez foarte mult lățimea unui dreptunghi raportat la lungimea sa, sau ce se întâmplă dacă lungesc foarte mult un dreptunghi raportat la lățimea sa? Pot spune că în ambele cazuri dreptunghiul tinde către o dimensionalizare liniară sau monodimensionalizare? De asemenea, ne putem întreba ce se întâmplă dacă mențin lungimea relativ egală cu lățimea dreptunghiului și micșorez sau măresc aria dreptunghiului? În cazul micșorării ariei, dreptunghiul devine o suprafață reletiv adimensională, în timp ce în cazul măririi ariei, el devine o suprafață bidimensională? Există o echivalare geometrică a acestor tipuri de alterări dimensionale? La momentul respectiv am postat aceste întrebări pe Quora și am primit niște răspunsuri frustrate, cum că noțiunile pe care mi le imaginez și cazurile în care apar aparțin, probabil, domeniului științifico-fantasticului, sau că încurc semnificații și exprimări diferite ale noțiunii de dimensiune. Eu însă nu am renunțat niciodată la la intuițiile mele despre relativitatea dimensională a suprafețelor în context compozițional, care s-au concretizat în metoda categoriilor elementar-dinamice, prezentată în EXPO 2-TOPOLOGIE (2). Atunci, însă, a trebuit să mă mulțumesc doar cu exprimarea modelării suprafețelor pusă la dispoziție de cazurile transformărilor geometrice.
Ele sunt de două tipuri: rigide și non-rigide, și presupun o corespondență între suprafața inițială, de referință, numită pre-imagine, și suprafața finală, remodelată, numită imagine, prin diferite procedee.
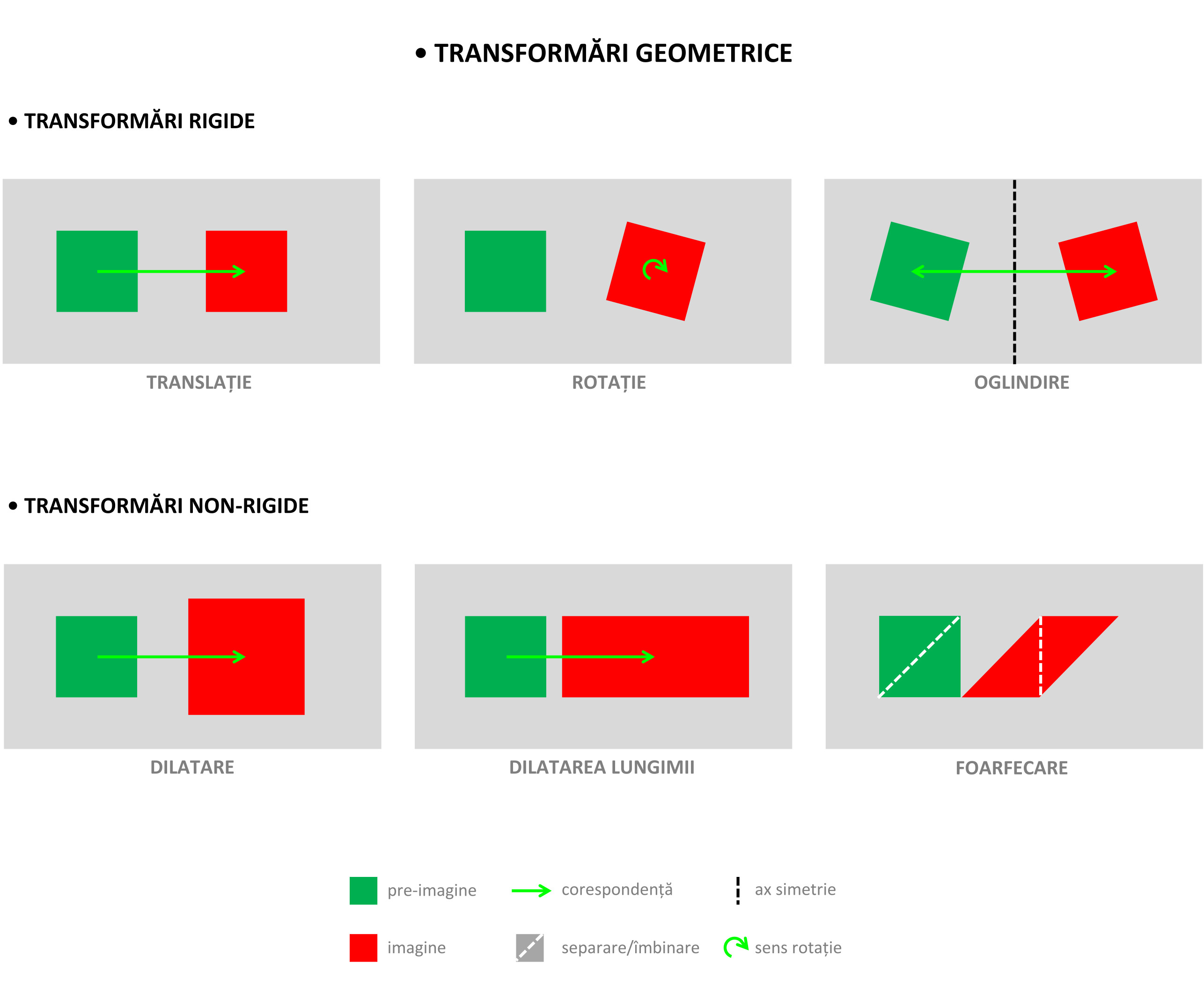
Rămân însă întrebări fără răspuns. Care este lungimea exactă a laturilor dreptunghiului în raport cu înălțimea sa pentru determinarea limitei dintre adimensionalizare și bidimensionalizare? Care este raportul dintre lungimea și lățimea dreptunghiului pentru aflarea limitei dintre caracterul regulat și cel neregulat al modelării sale? Care este raportul dintre aria dreptunghiului și cea a fondului pentru a determina caracterul adimensional, respectiv bidimensional al dreptunghiului? La aceaste întrebări nu există un răspuns algebric, pentru că metoda transformărilor este pur euclidiană și nu implică relativitate dimensională. Totuși, chiar dacă ar fi oferit, răspunsul ar caracteriza doar suprafețe individuale și nu suprafețele în context dinamic implicit.
3) Complexul elementar-dimensional
După cum putem observa, revine de fiecare dată problema definirii contextului compozițional. Ce este contextul compozițional și cum poate fi urmărit? Am văzut că nu poate fi surprins prin formule algebrice și nici prin simple rapoarte sau proporții între valori cantitative măsurate și rezultate din transformarea suprafețelor. Astfel, din experiențe repetate de contact cu materialul constructiv-componențial al suprafețelor – conținuturi și limite – a rezultat o intuire a unor principii de ordonare pozițională a categoriilor elementare și de caracterizare dimensională a suprafețelor, indiferent de caracteristicile lor măsurabile și proporționarea lor algebrică.
Astfel:
- orice suprafață absolută este bidimensională, dar în anumite condiții (nespecificate) de context spațial-compozițional ea poate deveni relativă adimensională sau relativă monodimensională;
- orice suprafață adimensională relativă este inclusă într-o suprafață bidimensională, care este mărginită de o suprafață monodimensională relativă;
- orice suprafață monodimensională relativă se formează la intersecția a două suprafețe bidimensionale, mărginite la rândul lor de suprafețe relative monodimensionale;
- orice suprafață adimensională relativă se formează la intersecția a două suprafețe monodimensionale.
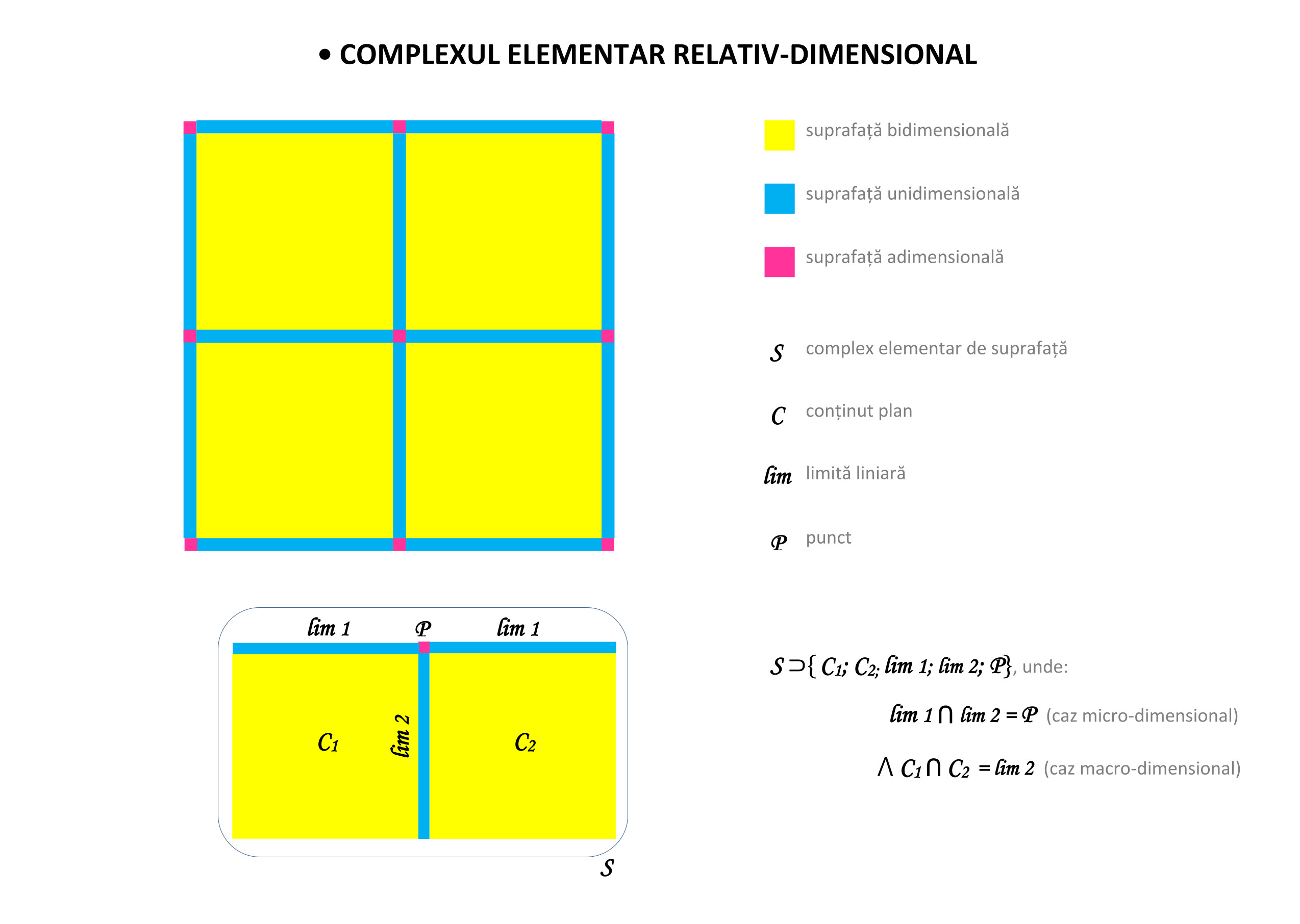
Rezultă astfel un complex de suprafețe cu caracter stabil elementar-dimensional și pozițional de succesiune și juxtapunere care poate fi descris topologic prin operații proprii limbajului mulțimilor. Problema acestei rezolvări este însă faptul că privitorul este pus în fața faptului împlinit, al dimensionalizării suprafețelor categorizate elementar, fără a i se oferi indiciile proceselor care au dus la aceste rezultate topologice, și nici instrumentarul prin care s-a obținut dimensionalizarea contextuală a suprafețelor în complexul compozițional. Este o metodă brută și necizelată. În plus, după cum vom observa, implicațiile sale nu sunt sintetice, ci analitice.
4) Metoda vectorială
S-ar putea argumenta că vectorul ca soluție a exprimării mișcării aparente ar fi cel mai evident lucru posibil – dar există un impediment care ar trebui să fie la fel de evident. Mișcarea implicită se aplică compoziției imaginilor statice, nu cinematice. De aceea vectorul atașat unui obiect static naște speculații privind adaptarea proprietăților sale cinetice – care în fizică au ca scop exprimarea mișcării pe baza vitezei și a accelerației mobilului – la nevoia de exprimare a dinamicii implicite sau aparent-pozițională prin simpla comparare a cantităților plasate de o parte și alta a obiectului pe traseul său de simetrizare. Ceea ce surprinde de fapt vectorul în mod esențializator în cadru formei este însuși sensul obiectului.
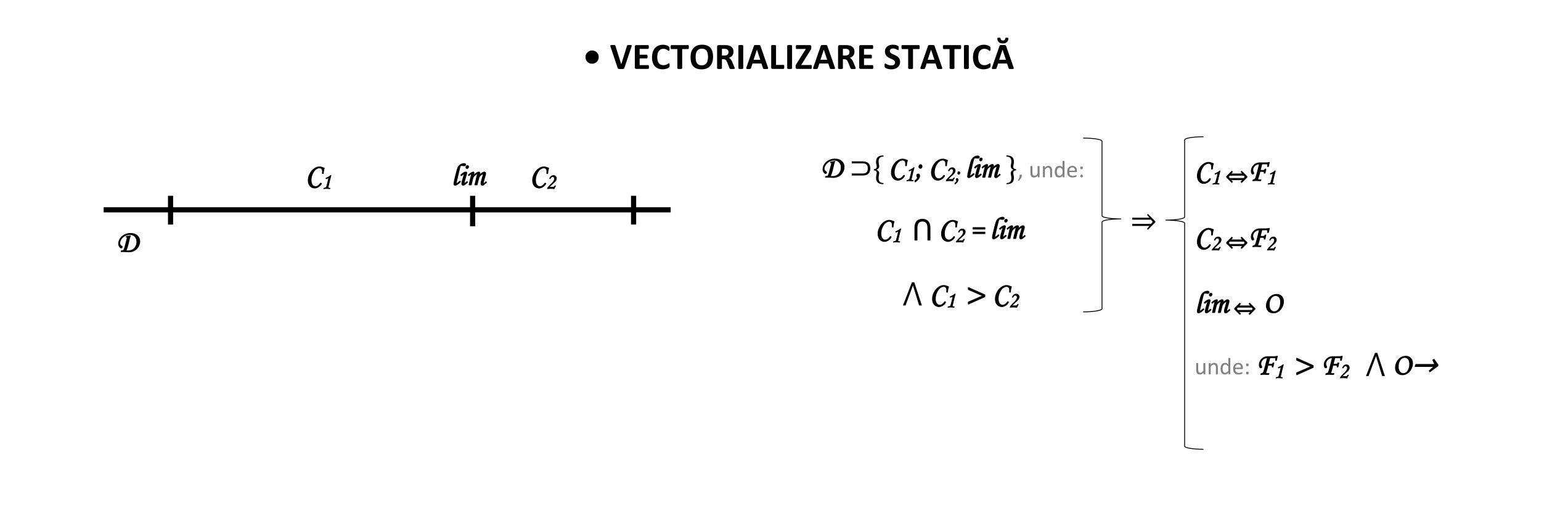
Cu toate acestea, vectorul în sine, ca instrument de esențializare morfologică, are un caracter reductiv epi-fenomenal. Ceea ce înseamnă că, deși pune în evidență forma – care este o sinteză atentivă a componentelor constructive ale suprafețelor compuse – caracterul său aplicativ este analitic, pentru că vizează fiecare limită constructivă a suprafețelor compoziționale.
5) Metoda medianei
Deși nu am planificat inițial această metodă în detaliu, a trebuit să o practic și să o perfecționez pe parcursul cercetării și ordonării materialului constructiv al temelor complexe, nevoit fiind să concentrez etapele pentru rezolvarea sintetic-morfologică a construcției suprafețelor. Ea implică un arsenal de convenții care s-au clarificat pe parcurs, odată cu necesitatea sporirii clarității de exprimare a iterărilor componentelor morfologice.
Dincolo de stadiile de elaborare a metodei medianei, care pot fi observate în succesiunea tematică a cazurilor aplicative, voi prezenta mai jos doar convențiile finalizate ale aplicării metodei în dezvoltarea iterărilor morfologice.
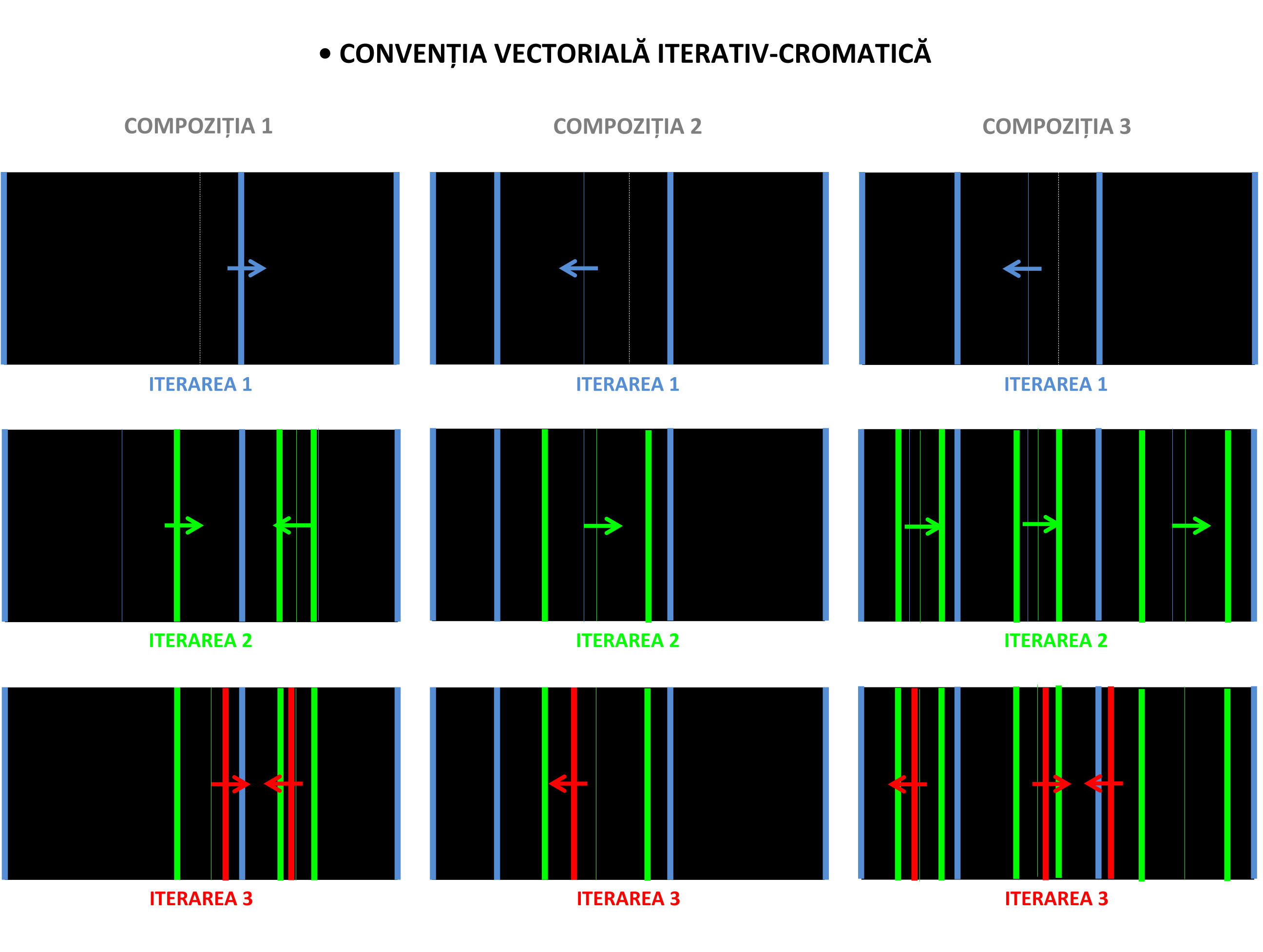
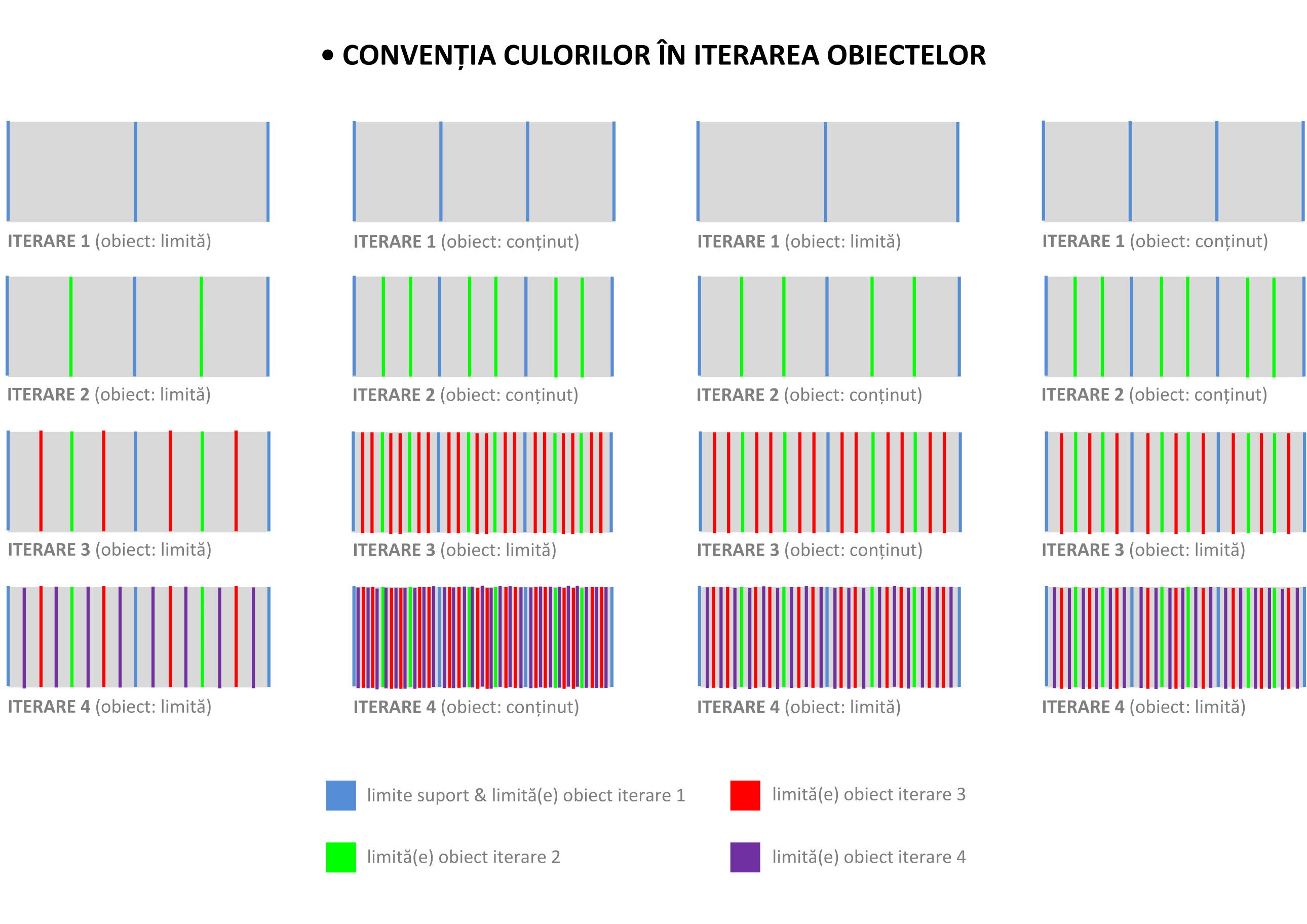
Vizualizând modelele putem concluziona următoarele principii de convenționalizare:
- principiile de convenționalizare cromatică pot fi aplicate pe toate tipurile de dezvoltări morfologice: co-iterative, trans-iterative și infra-iterative;
- pentru patru iterări consecutive, introoduse ierarhic începând cu iterarea de bază, până la cea superioară, se vor folosi următoarele culori: albastru deschis, verde fosforescent, roșu vermillon și ,respectiv, violet;
- fiecare nouă culoare va fi aplicată pe obiectul unei noi iterări complete (obiect cu suport de fond);
- limitele componentelor morfologice vor fi notate cu linii continue groase, iar medianele dintre limitele componentelor morfologice vor fi notate prin linii continue subțiri;
- vectorii atașați de mediane și limite vor avea aceeași culoare cu acestea.
În concluzie, metoda medianei are ca finalitate cel mai înalt grad de valorificare a metodei vectoriale în sensul sintezei și esențializării morfologice, apropiindu-se cel mai mult de idealul pur observațional de aplicare al ceretării morfo-structurale vizuale – în timp ce valorificarea dimensională a metodei vectoriale este una analitică și fără o finalitate directă morfo-atentivă. În plus, deși putem înțelege structura morfo-iterativă a compoziției ca fiind fractalică și finită, metodele dimensiunii fractalice nu oferă decât o exprimare cantitativ-numerică și o formulare potențială algebrică a acoperirii cromatice a suprafețelor compuse, ignorând modelarea lor.
OBSERVAȚIE FINALĂ:
În afară de metoda medianei, care este valorificarea sintetic-esențializatoare a metodei vectoriale, toate metodele au ca finalitate relativizarea dimensional-elementară a suprafețelor în context compozițional, dintre care doar metoda vectorială reușește să o surprindă în mod organic. Această finalitate relativizatoare este însă ea însăși doar o limită EMPIRICĂ în înțelegerea topologiei compoziționale, care ar trebui aprofundată mult mai serios din punct de vedere MATEMATICO-ATENTIV, folosind principiile teoriei mulțimilor într-o viitoare EXPO 3.
SURSELE IMAGINILOR EDITATE:
GIOVANNI BATTISTA MORONI: CROITORUL, 1565-1570
https://www.nationalgallery.org.uk/paintings/giovanni-battista-moroni-the-tailor-il-tagliapanni
GEORGES DE LA TOUR: SFÂNTUL IERONIM ÎN RUGĂCIUNE, 1642
https://gallerix.org/pic/T/1880358061/768240964.jpeg
DIEGO VELÁZQUEZ: FEMEIE BĂTRÂNĂ GĂTIND OUĂ, 1599 - 1660
RAFAEL SANZIO: LOGODNA FECIOAREI, 1504
PIETRO PERUGINO: LOGODNA FECIOAREI, 1500-1504
https://uploads7.wikiart.org/00129/images/pietro-perugino/marriage-of-the-virgin.jpg!Large.jpg
METODA NUMĂRĂRII CUTIILOR: HARATA MARII BRITANII
https://demonstrations.wolfram.com/BoxCountingTheDimensionOfCoastlines/
METODA NUMĂRĂRII CUTIILOR: MODELUL MORFOLOGIC
https://python-fiddle.com/?checkpoint=1747325781
METODA NUMĂRĂRII CUTIILOR: G. B. MORONI: CROITORUL
https://chatgpt.com/c/6826174b-a374-800f-822c-c03850d8c8e1