APPLICATIONS (CODA & APPENDIX)

CODA
I delayed persistently the finalization of this last applied exposition because dealing with complex themes requires a much more sustained effort of synthesis than I expected, but, paradoxically, a much more precise analytical preparation by selecting the most concise variants of deconstruction and contiguity of surfaces. However, I still have reservations and believe there is room for a much more direct approach, even at the risk of declining geometric accuracy. The application of the median method suggests a closer approach to the goal of a purely observable approach in visual-structural morphological research due to the reduction of surface processing. However, this approach remains a goal for the more distant future due to the complexity of the analytic information and the need for new, more comprehensive reduction criteria - such as statistical ones.
As mentioned in the concluding remarks in the first part of the applications, a consistent simplification of the steps was needed, even if this means a concentration of the analysis in the phases originally intended for the morphological synthesis. To this end, we have abandoned the vectorialization of limits and the elementarization of contents. Initially, we thought that the tendencies of dimensional elementarization of surfaces would help to indicate morphological objects by dimensional recessivity and dimensional alternation between background-object-background. Despite this, the vectoriality of boundaries does not imply by direct effect the sense of morphological object content.
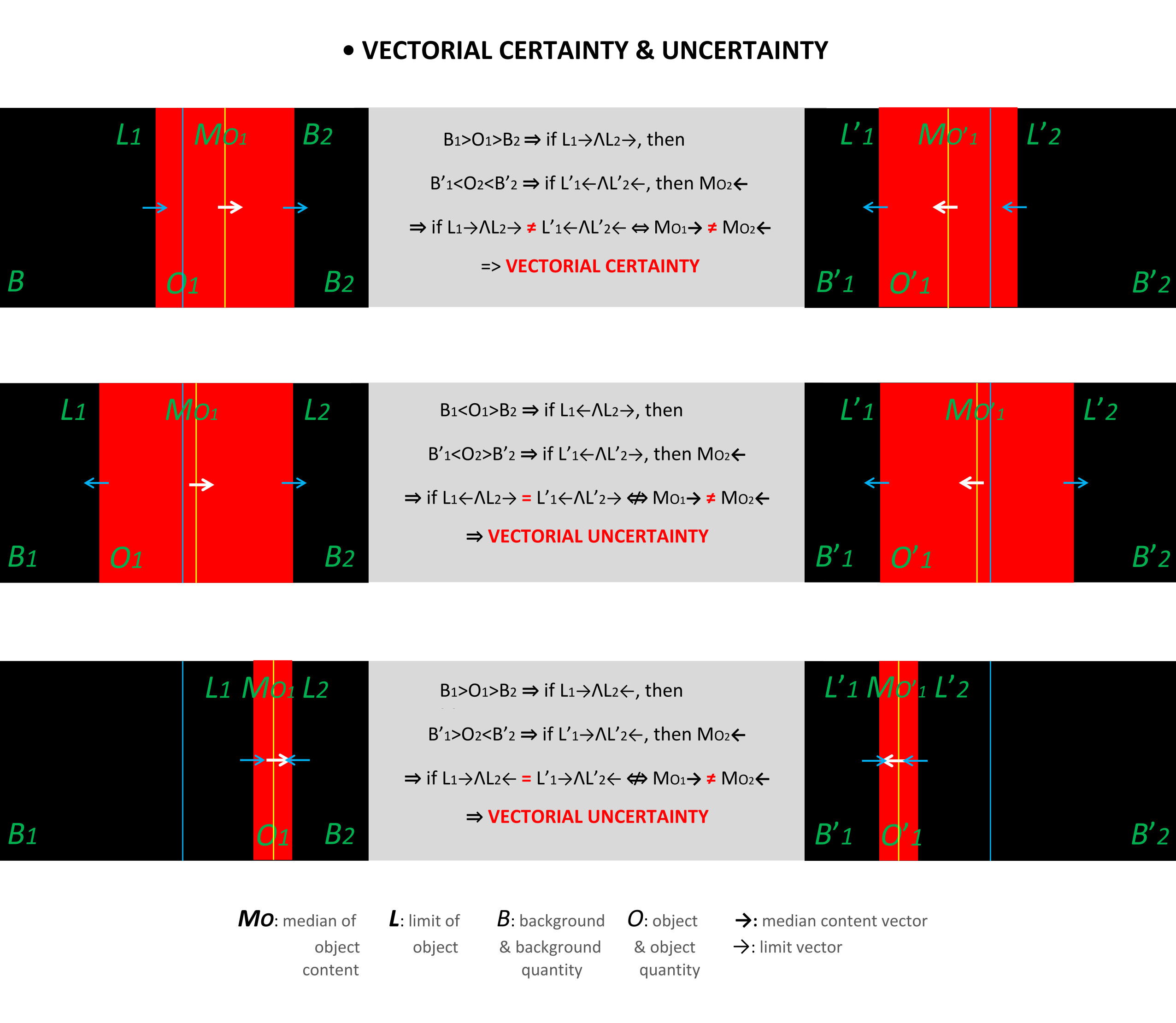
We can find the vectorial sense more accurately by observing the median of the object content relative to the median of its support surface, including the object and the background, complementary to the direction of their collinearity path.
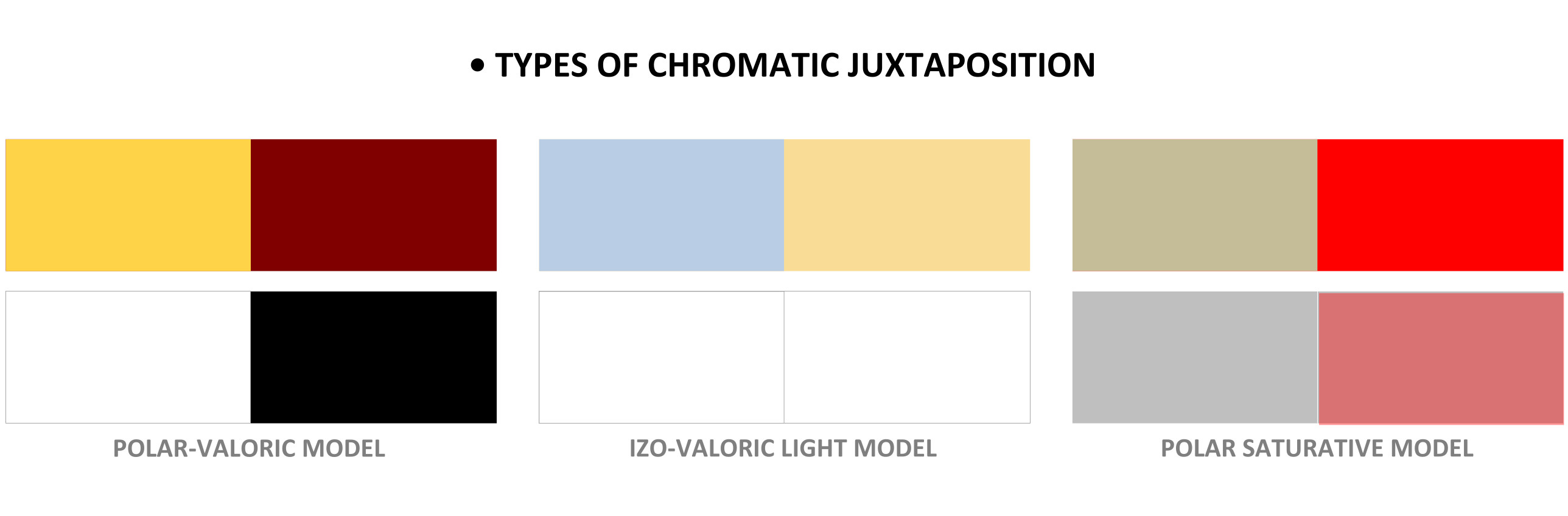
Emphasis falls on the contour delineation of surfaces using the categories of oblique rectilinear directions deduced by simplifying the organic limits of the chromatic map surfaces. The complex fragmentation of the surfaces, however, requires their deduction from the overall geometric relationships of the network traces of the work support. Also, we can simplify the chromatic maps by replacing tonal diversity and chromatic categories with relations of value polarity, saturative contrast, and caloric contrast, emphasized by iso-value integration, with dark or light dominance.
To merge the stages of the synthesis initiation, we will combine the deconstruction of surfaces with their collinearization. At this incipient level of construction morphological processing, there is no single solution but multiple possibilities within the horizon of elegance and unity of contiguity in the organization of surfaces by comprehensive and easy-to-decipher morphological collinear trajectories.
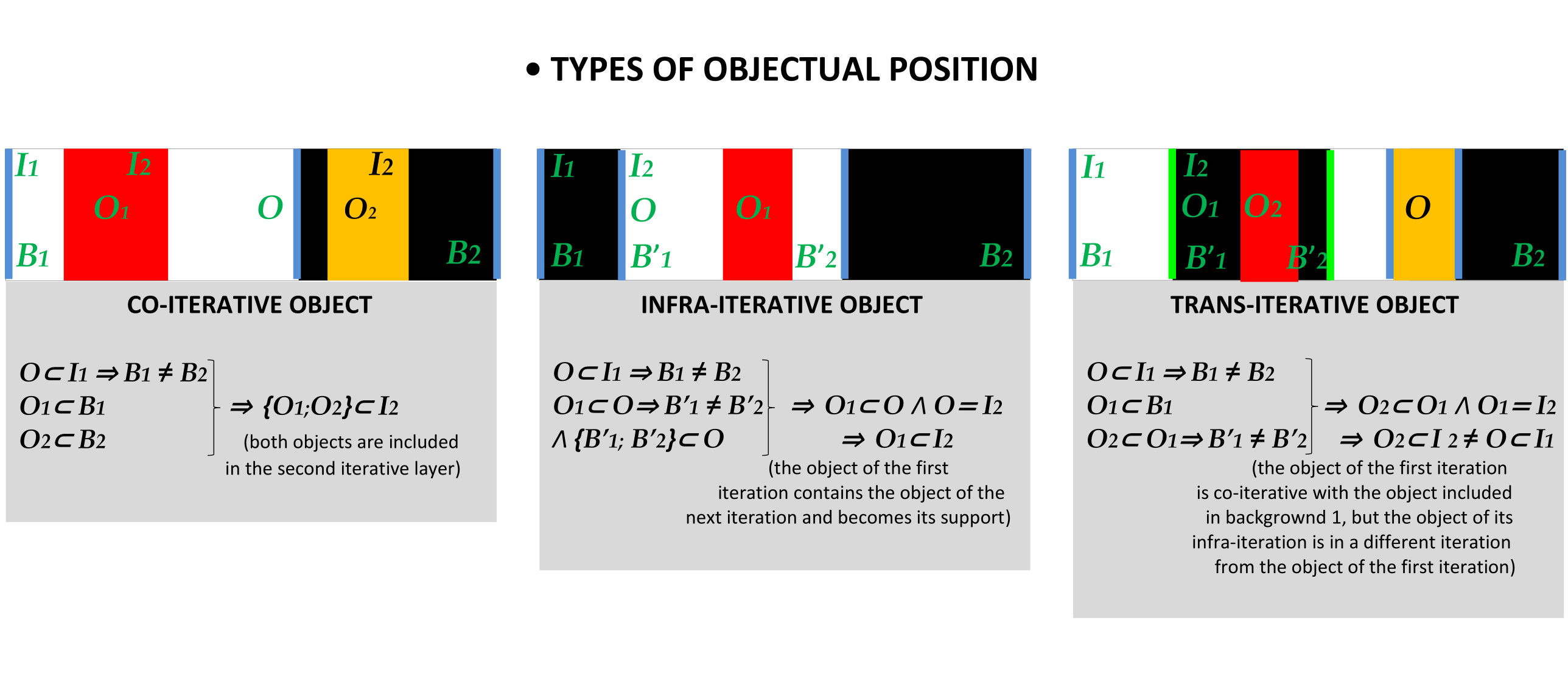
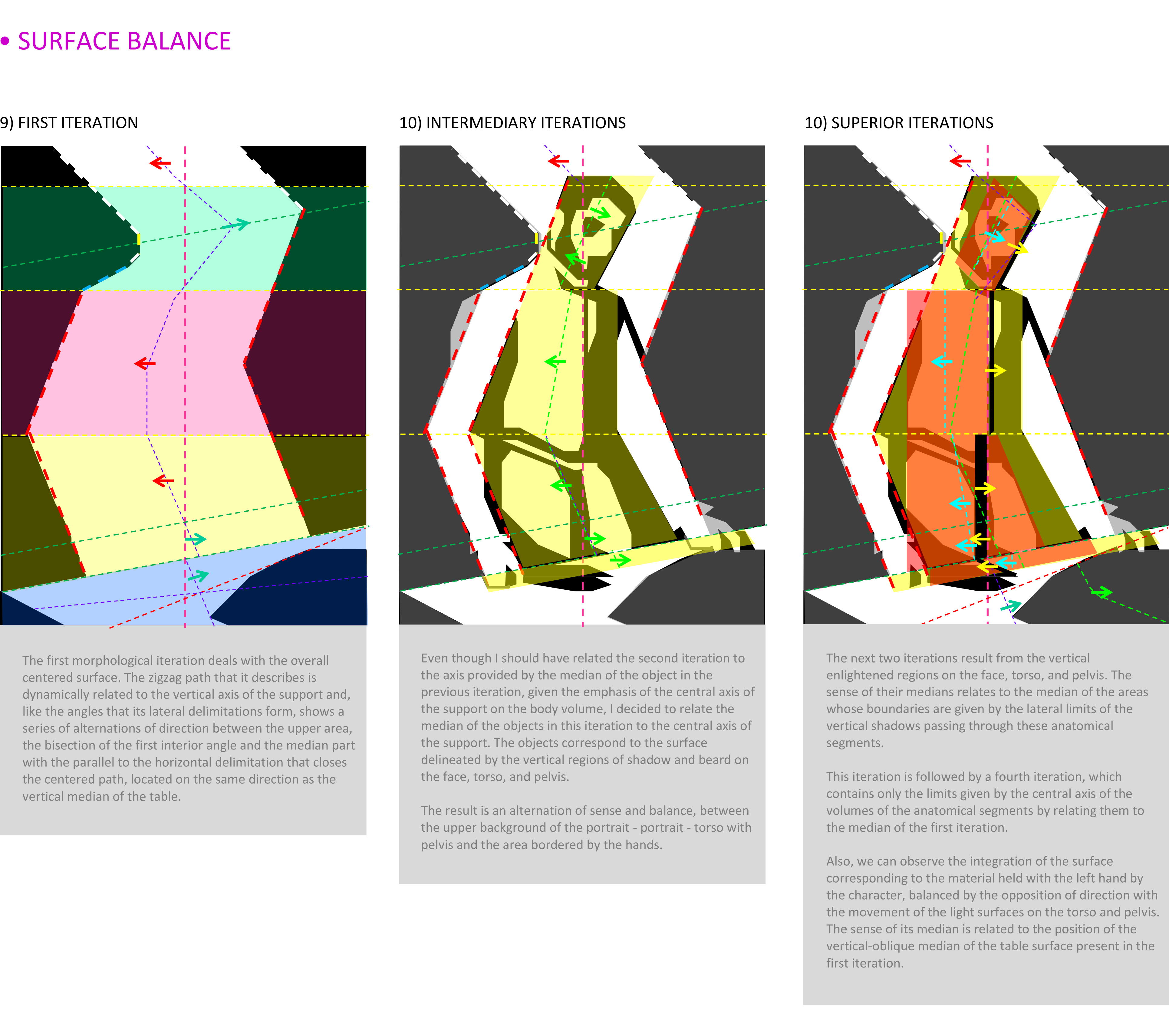
The balance of the morphological iterations is the final stage of essentialization for the morphological synthesis of construction, realized by deciphering the meaning and hierarchy of the objects. From a hierarchical point of view, each form belongs to an attentional-selective layer called morphological iteration, which results in three types of connections between forms and objects:
1) co-iterative, with objects placed in forms developed at the same iterative level but inside distinct morphological components of the same basic form;
2) trans-iterative, with objects placed in distinct iterations, developed in distinct morphological components of the base form;
3) infra-iterative, with objects placed in forms developed in successive and recurrent iterations, included in the same morphological component of the basic form.
Following these simplifications of the morphological research stages, we will reduce the entire laborious sequence of twelve steps to only four or six steps. We will see, however, that there is no predetermined path of morphological deciphering in complex themes. Each work and each author has peculiar morphological subdivision procedures, more or less accessible through reduction. They depend on the selective visual interests for the constructive material of the composition.












APPENDIX
Before setting up the vectorial method, applied to the limits and contents of surfaces in the compositional context of quantitative variations, I tried to solve the problem of expressing the compositional context by other methods with a more pronounced mathematical and measurable or enumerative, non-dynamic character. The main constructive clues in the mathematical definition of form at that time were the fractal features due to the iterative deepening of the morphological components, and the contextual-dimensional manifestation of the composition's surface modeling. In the first tendency, we include the methods of fractal dimensionalization and surface compartmentation by nesting and packing, while the second tendency covers the surface transformation method. As a mixed method, which combines fractal recurrence and geometric surface dimensionalization, we have the elementary-dimensional complex, which led to the need for the discovery of the vectorial method.
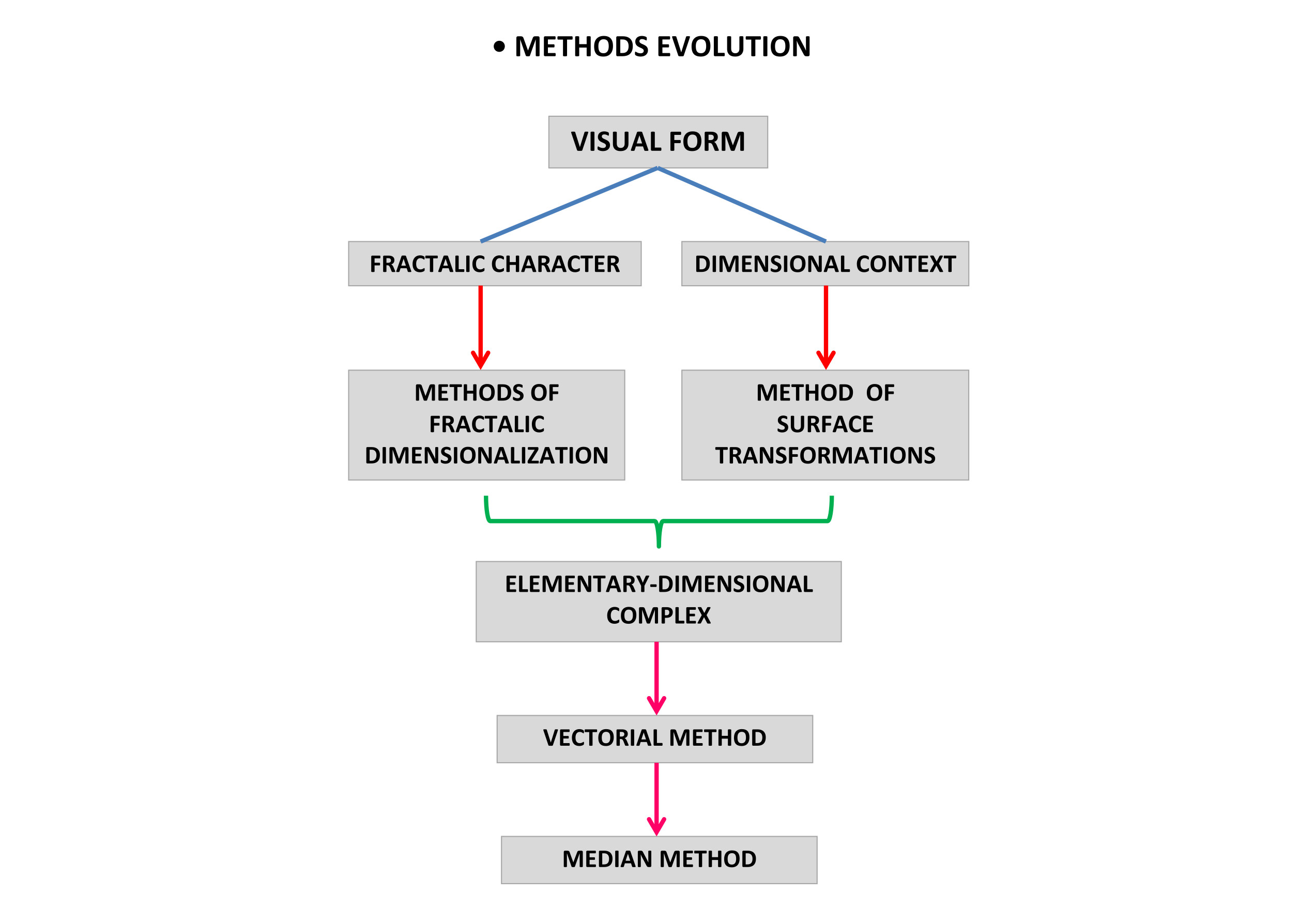
Finally, given their synthetic character, only the vectorial method and mostly the median method proved to be the most suitable for the essentialized expression of the implicit motion of surfaces in the compositional context. The application of the scalar and transformational methods proved to be too vague, respectively, too rigid, and, consequently, incompatible with the synthetic and essentialized-reductive exploration of surface relations in the compositional context.
1) Fractal dimensionalization
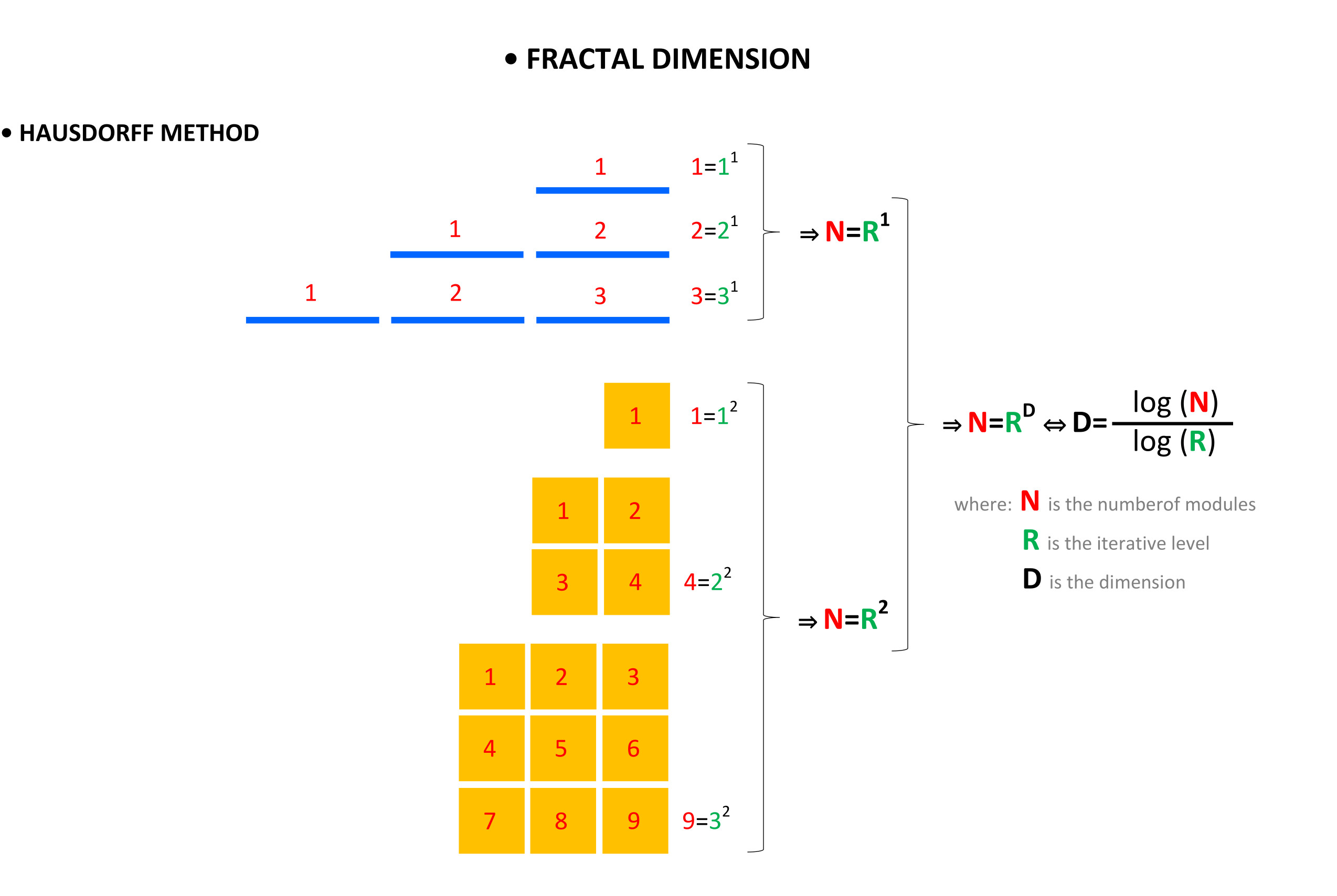
Given the modular organization of the construction of the morphological components, we can describe the visual form as a one-dimensional scalar fractal, where instead of line segments, we have rectangles as a module. In this case, we would apply the Hausdorff method of calculating the fractal dimension by scalarization, and its dimension would be equal to 1. In the case of value polarization, we can obtain a white object on a black background, and applying the box-counting method, we express the ratio between black and white surfaces as a dimension approximately equal to 1.98.
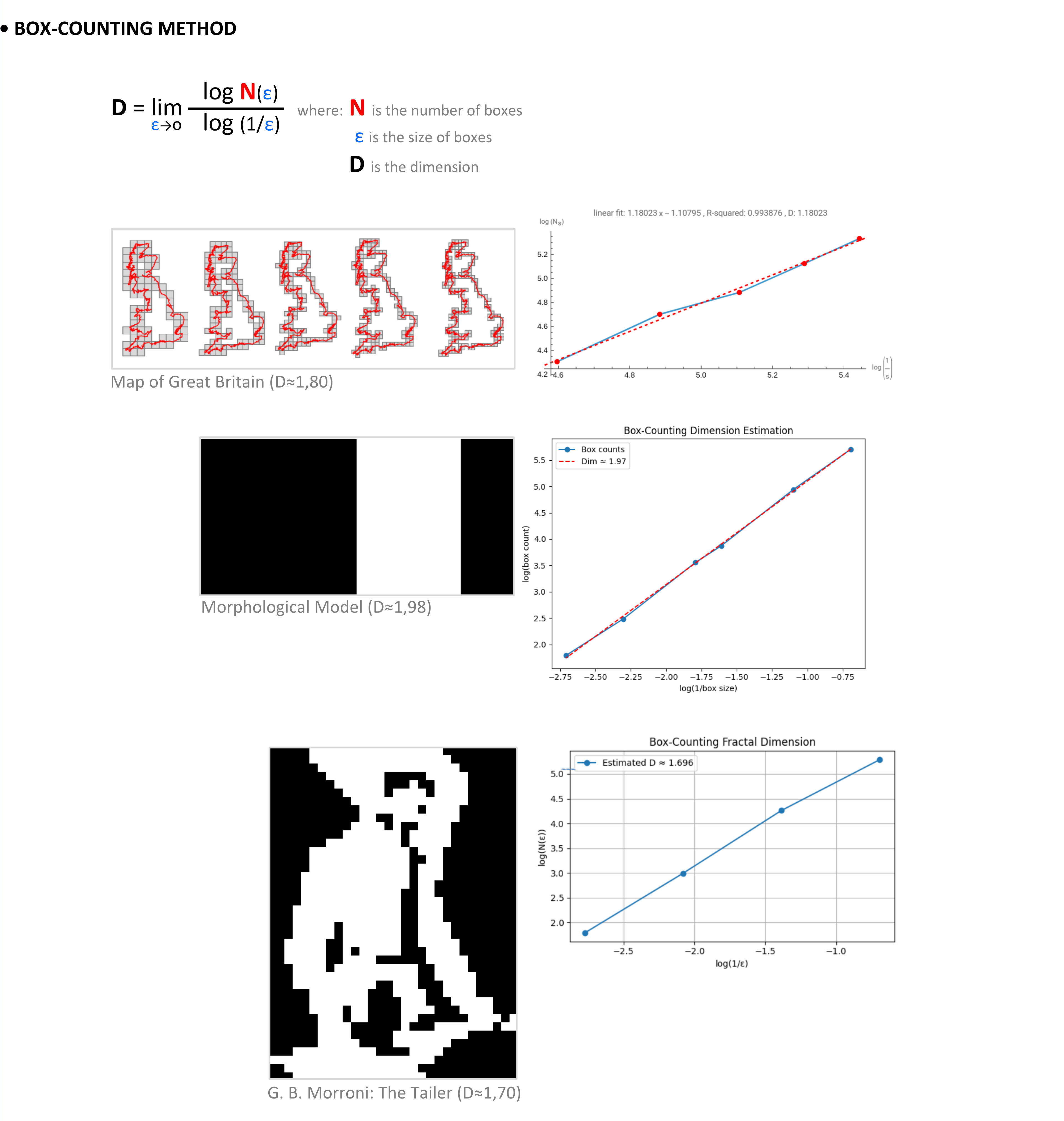
As a further development of the Haudorff method, we can use methods of deconstructive surface compartmentation by raking the small side on the large side of a rectangle or by nesting and packing methods. Nesting involves making the space of the compartmentalized surface content more effective, while packing is based on exploiting as much space as possible, leading to a higher degree of content filling.
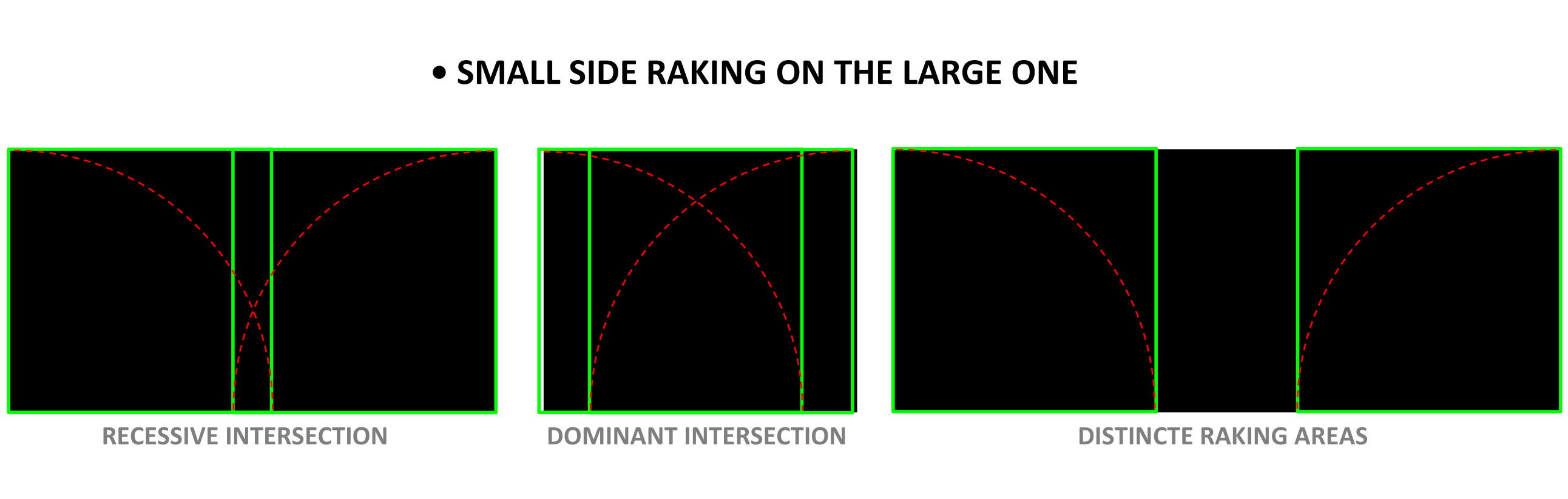

Algebraic expressions for the degrees of coverage of a morphological surface relative to another surface, although they can be dimensionally comparable, cannot describe the positioning and dynamics of surface patterning. In fact, at the time these methods were proposed, the dynamics of surfaces were only intuited.
2) Surface transformation
What if I make the width of a rectangle very narrow relative to its length, or what if I make a rectangle very long relative to its width? Can I say that, in both cases, the rectangle tends towards linear or monodimensionalization? We can also ask what happens if I keep relatively equal sights of the rectangle while decreasing or increasing its area. In the case of decreasing the area, the rectangle becomes a monodimensional relative surface while increasing the area, it becomes a two-dimensional surface. Is there a geometric equivalence between these types of dimensional alterations? At the time, I posted these questions on Quora, receiving some frustrated responses that the notions I was imagining and the cases in which they occur probably belong to the realm of science fiction or that I confused different meanings and expressions of dimension notion. However, I have never given up my intuitions about the dimensional relativity of surfaces in a compositional context, which materialized in the method of elementary-dynamic categories presented in EXPO 2-TOPOLOGY (2). Then, however, I had to content myself only with the expression of surface modeling provided by the cases of geometric transformations.
They are of two types, rigid and non-rigid, and imply a correspondence between the initial reference surface, called the pre-image, and the final, remodeled surface, called the image, by various processes.
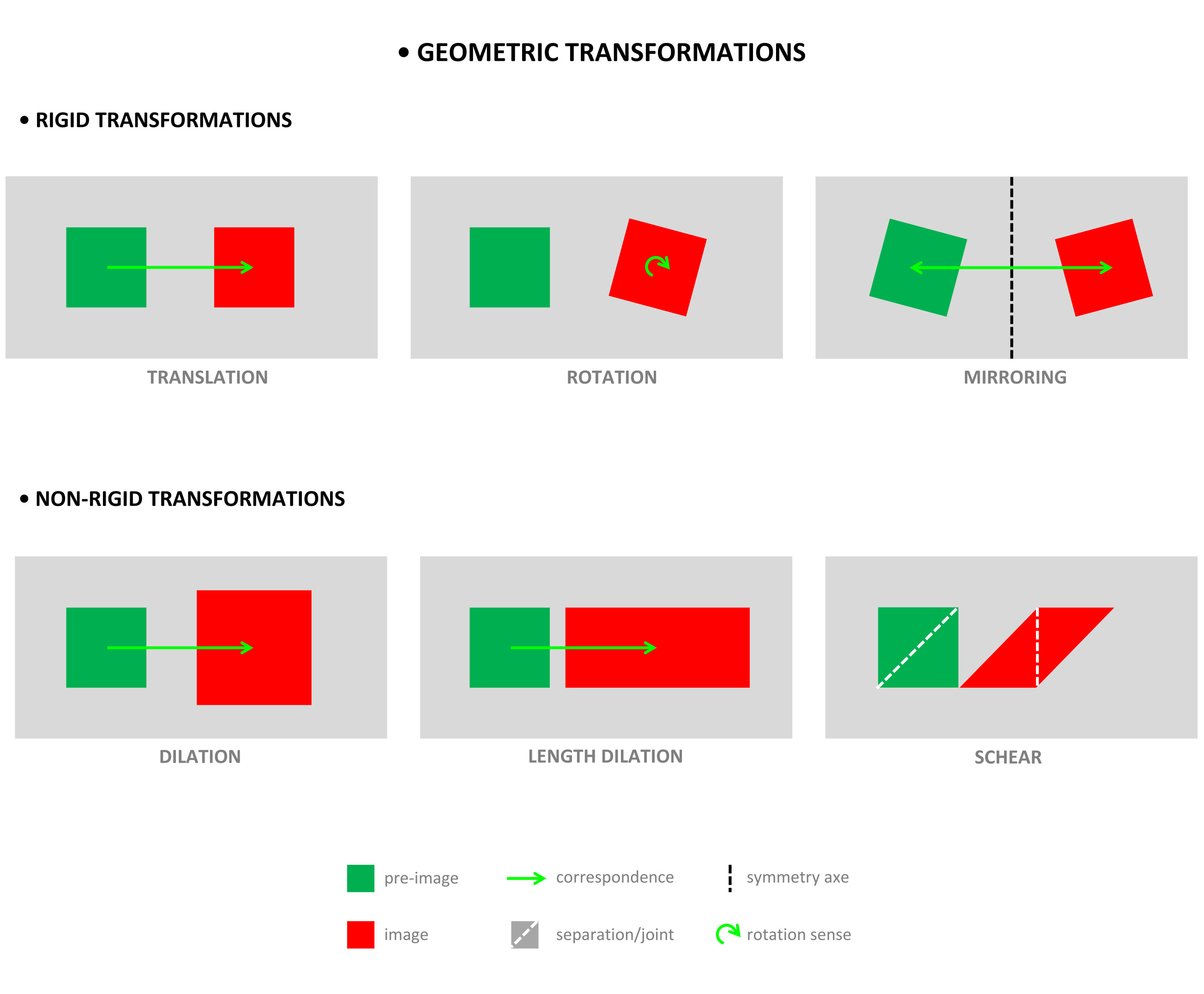
But unanswered questions remain. What is the exact length of the sides of the rectangle related to its height for determining the boundary between dimensionlessness and two-dimensionality? What is the ratio between the length and width of the rectangle to find the boundary between the regular and irregularity of its modeling? What is the ratio between the area of the rectangle and the area of the background to determine the a-dimensionality and the two-dimensionality of the rectangle? These questions have no algebraic answer because the method of transformations is purely Euclidean and does not involve dimensional relativity. However, even if offered, the answer would characterize only individual surfaces and not surfaces in the implicit dynamical context.
3) Elementary-dimensional complex
As we can see, the problem of defining the compositional context arises repeatedly. What is compositional context, and how can it be traced? We have seen that it cannot be grasped by algebraic formulas nor by simple ratios or proportions between measured quantitative values and those resulting from the transformation of surfaces. Thus, from repeated experiences of contact with the constructive-componential material of surfaces - contents and limits - an intuition of principles of the positional ordering of elementary categories and dimensional characterization of surfaces, regardless of their measurable characteristics and their algebraic proportioning, has resulted.
Thus:
- any absolute surface is two-dimensional, but under certain (unspecified) compositional conditions of spatial context, it can become two-dimensional relative or one-dimensional relative;
- any relative two-dimensional surface belongs to a two-dimensional surface bounded by a one-dimensional relative one-dimensional surface;
- any one-dimensional relative surface results at the intersection of two two-dimensional surfaces, which are in turn bounded by relative one-dimensional one-dimensional surfaces;
- any relative a-dimensional surface is formed at the intersection of two one-dimensional non-collinear surfaces.
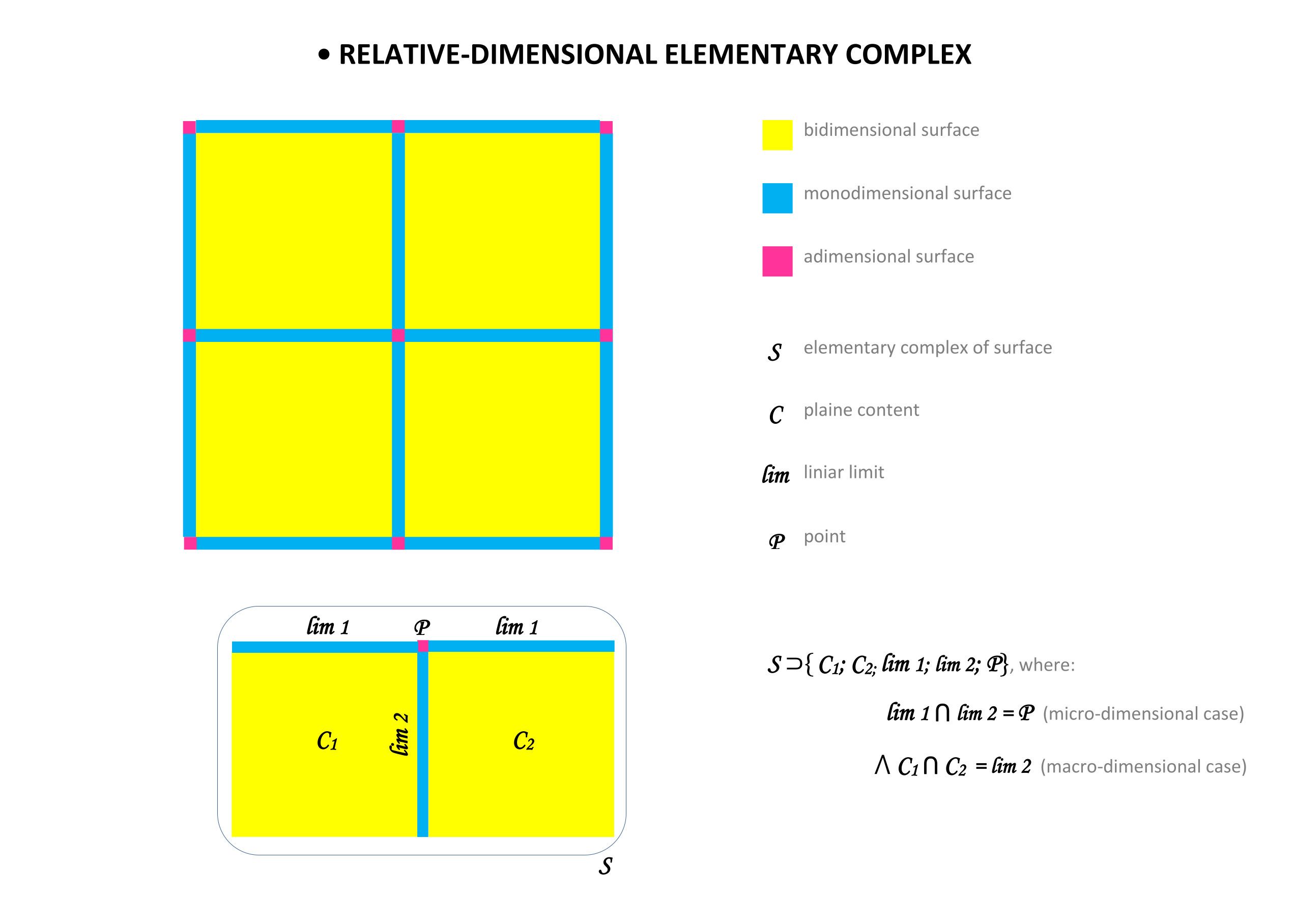
The result is a complex of surfaces with a stable elementary-dimensional and positional character of succession and juxtaposition that can be described topologically by operations belonging to the principles of set theory. The problem with this resolution, however, is that the viewer takes contact with the accomplished fact of the elementary categorized surface dimensionalization without being given any clues to the processes that led to these topological results nor the instrumentation by which the contextual dimensionalization of surfaces in the compositional complex realized. It is a rough method. Moreover, as we shall see, its implications are not synthetic but analytic.
4) Vectorial method
One could argue that the vector as a solution for expressing apparent motion would be the most obvious thing possible - but there is an impediment that should be equally obvious. Implied motion applies to static, not kinematic, image composition. Therefore, the vector attached to a static object gives rise to speculation about adapting its kinetic properties - which in physics aim to express motion based on the velocity and acceleration of the moving object - to the need to express implicit or apparent and positional dynamics by simply comparing the quantities placed on either side of the object along its symmetrized path. What captures the vector in an essentialized way in the form frame is the very meaning of the object.
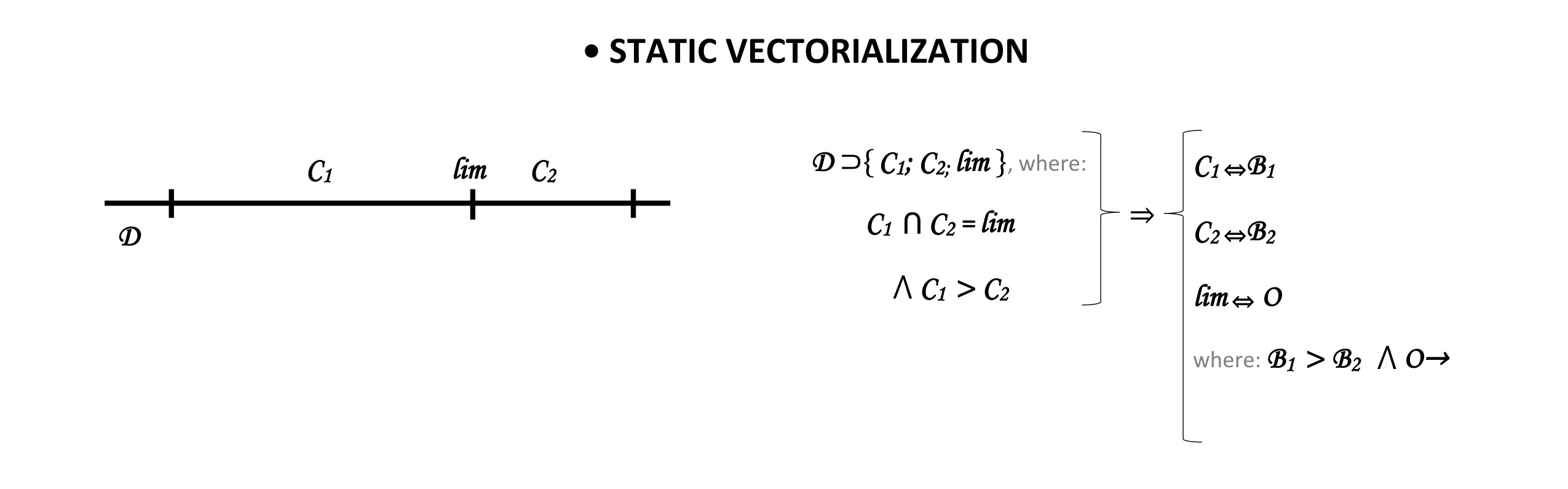
However, the vector itself, as a tool of morphological essentialization, has a reductively epi-phenomenal character. This means that although it emphasizes form as an attentional synthesis of the constructive components of compositional surfaces, its applicative character is analytic because it targets every constructive limit of compositional surfaces.
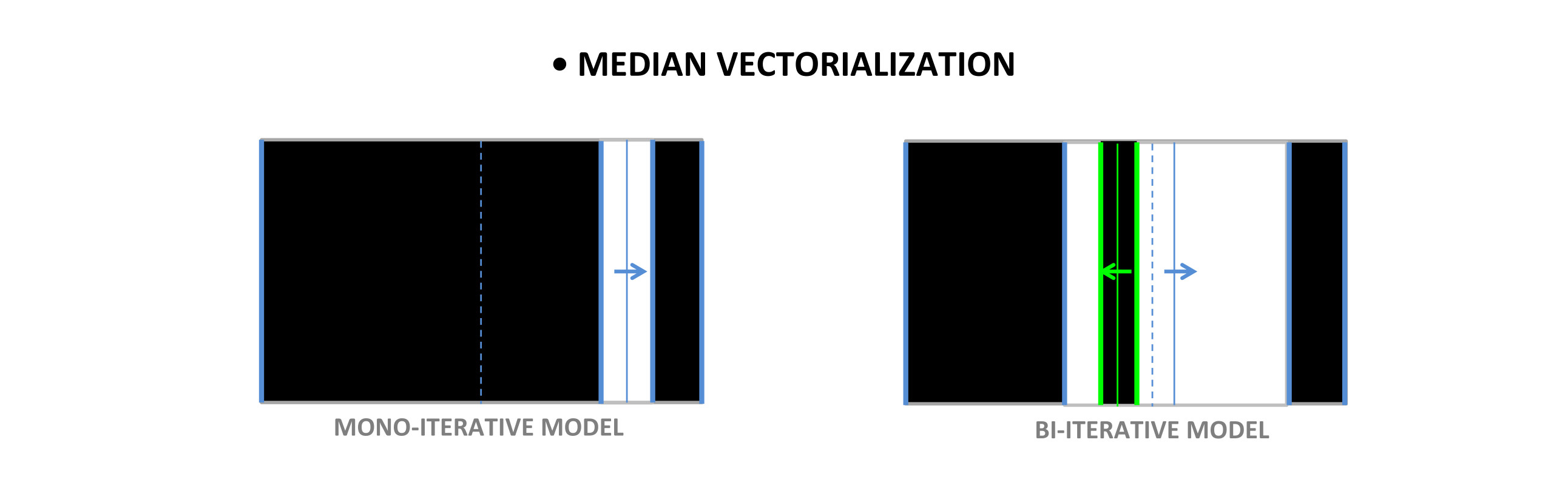
5) Median method
Although I did not initially plan this method in detail, I had to practice and refine it during the research and organizing of the constructive material for complex themes, forced to concentrate on the steps of the synthetic-morphological resolution of the surface construction. It involves an arsenal of conventions that have become clearer along the way, with the need to increase the clarity of expression for the iterations of the morphological components.
Beyond the stages of the development of the median method, which can be observed in the thematic succession of the application cases, I will present below only the finalized conventions of its application on the development of morphological iterations.
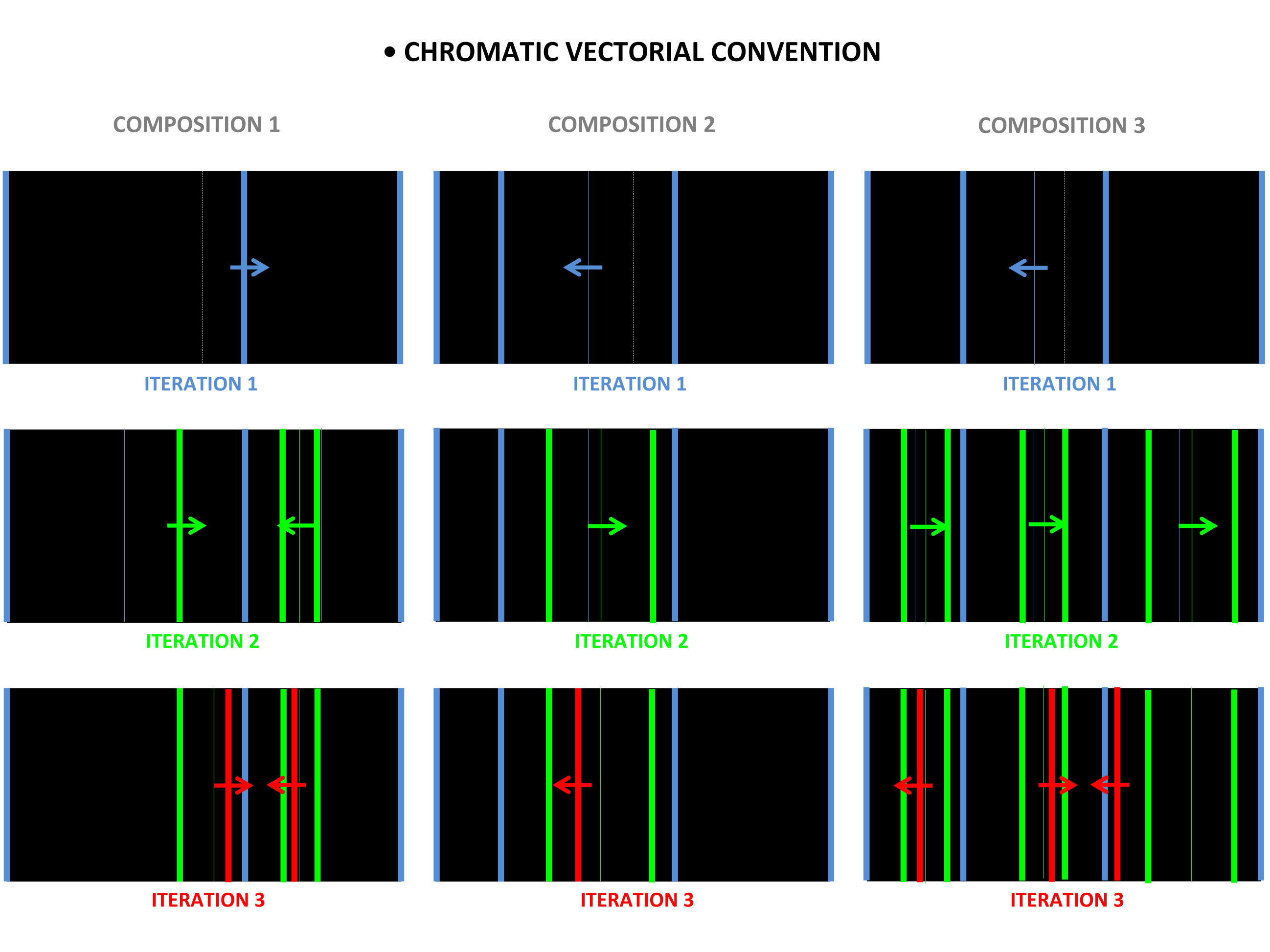
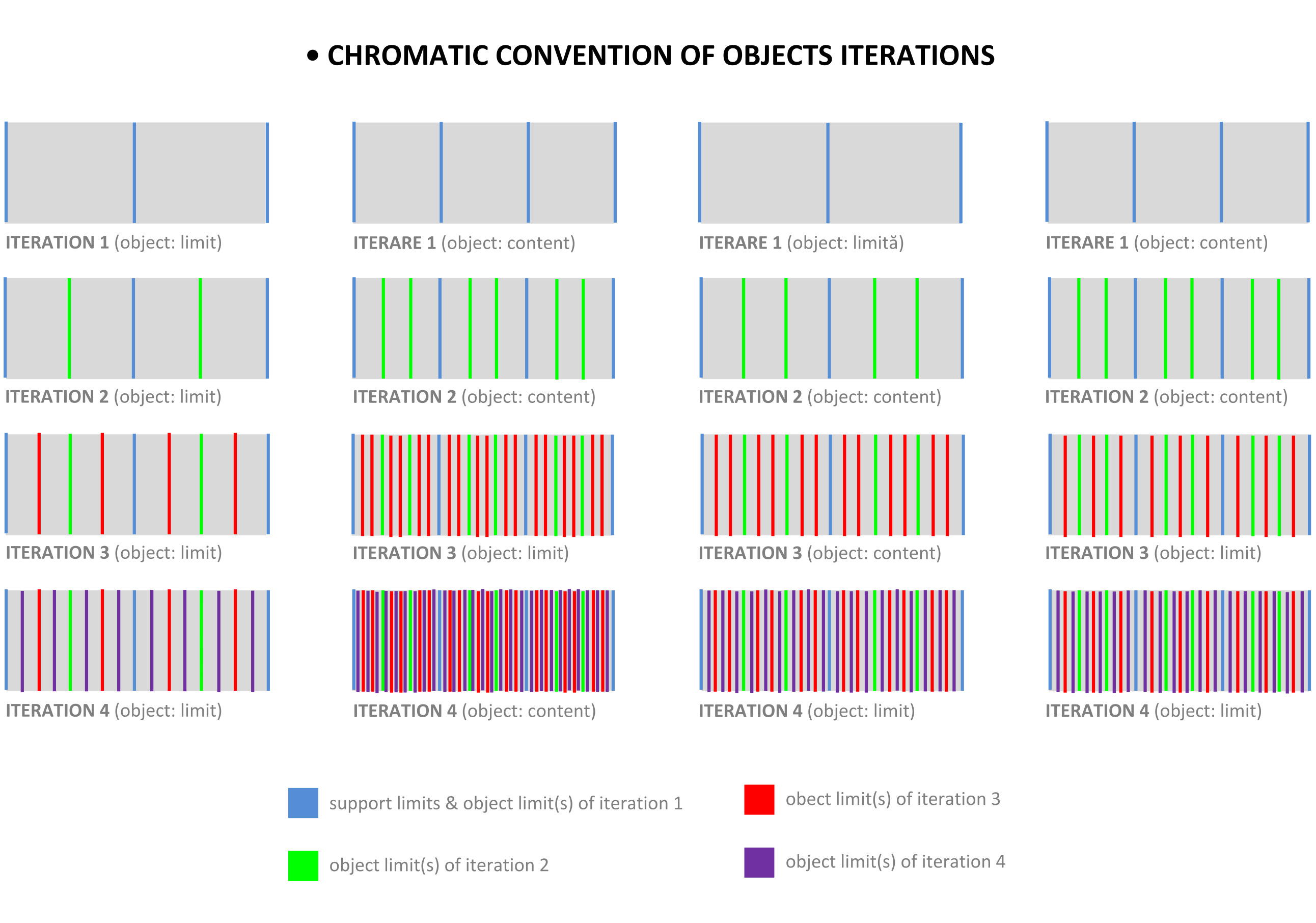
Visualizing the models, we can conclude the following principles of convention:
- we can apply the principles of chromatic convention to all types of morphological developments: co-iterative, trans-iterative, and infra-iterative;
- we will use light blue, phosphorescent green, vermilion red, and violet for the four consecutive iterations, introduced hierarchically starting from the base iteration up to the top iteration;
- we will apply each new color on the object of a new complete iteration (object with background support);
- we will denote the boundaries of the morphological components by thick solid lines and the median between the boundaries of the morphological components by thin solid lines;
- the vector attached to the median and boundaries will have the same color as them.
In conclusion, the median method has as its finality the highest degree of valorization of the vectorial method in the sense of morphological synthesis and essentialization, coming closest to the purely observational ideal of application of visual morpho-structural research – while the dimensional development of the vectorial method is analytical and without a direct morpho-attentional finality. Moreover, although we can understand the morpho-iterative structure of the composition as fractal and finite, the methods for fractal dimension provide only a quantitative-numerical expression and a potential algebraic formulation of the chromatic covering of the compositional surfaces, ignoring its modeling.
FINAL OBSERVATION:
Apart from the median method, which is the synthetic-essentializing valorization of the vectorial method, all the methods target the dimensional-elementary relativization of surfaces in a compositional context, out of whom only the vectorial method manages to capture it organically. However, the vectorial method per se is only an EMPIRICAL limit in understanding the compositional topology, which we will explore much more carefully from a MATHEMATICAL-ATTENTIVE point of view, using the principles of the set theory in a future EXPO 3.
SOURCES OF EDITED IMAGES:
GIOVANNI BATTISTA MORONI: THE TAILOR, 1565-1570
https://www.nationalgallery.org.uk/paintings/giovanni-battista-moroni-the-tailor-il-tagliapanni
GEORGES DE LA TOUR: SAINT JEROME AT PRAYER, 1642
https://gallerix.org/pic/T/1880358061/768240964.jpeg
DIEGO VELÁZQUEZ: OLD WOMAN COOKING EGGS, 1599 - 1660
RAFAEL SANZIO: THE MARRIAGE OF THE VIRGIN, 1504
PIETRO PERUGINO: THE MARRIAGE OF THE VIRGIN, 1500-1504
https://uploads7.wikiart.org/00129/images/pietro-perugino/marriage-of-the-virgin.jpg!Large.jpg
COUNTING-BOX METHOD: MAP OF GREAT BRITAIN
https://demonstrations.wolfram.com/BoxCountingTheDimensionOfCoastlines/
COUNTING-BOX METHOD: MORPHOLOGICAL MODEL
https://python-fiddle.com/?checkpoint=1747325781
COUNTING-BOX METHOD: G. B. MORONI: THE TAILOR
https://chatgpt.com/c/6826174b-a374-800f-822c-c03850d8c8e1